在一些有N个元素的集合应用问题中,我们通常是在开始时让每个元素构成一个单元素的集合,然后按一定顺序将属于同一组的元素所在的集合合并,其间要反复查找一个元素在哪个集合中。这就是在我们算法中经常使用的并查集算法
解决什么问题
- 将两个集合合并
- 询问两个元素是否在一个集合当中
基本原理
每个集合用一棵树来表示。树根的编号就是整个集合的编号。每个节点存储它的父节点,表示的父节点
初始化
- 将所有节点的父节点设为自己

int p[N];
for (int i = 1; i <= n; i++)
p[i] = i;
合并集合
- 将节点1合并到节点2形成一个集合,节点3和节点5合并到结点4形成一个集合
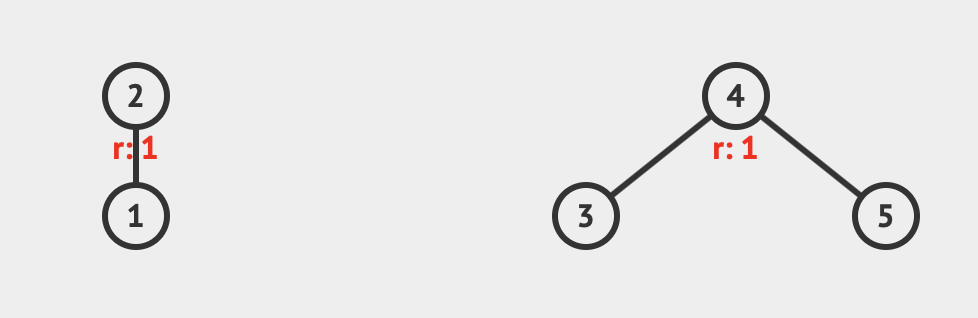
- 再将两个集合合并成一个集合
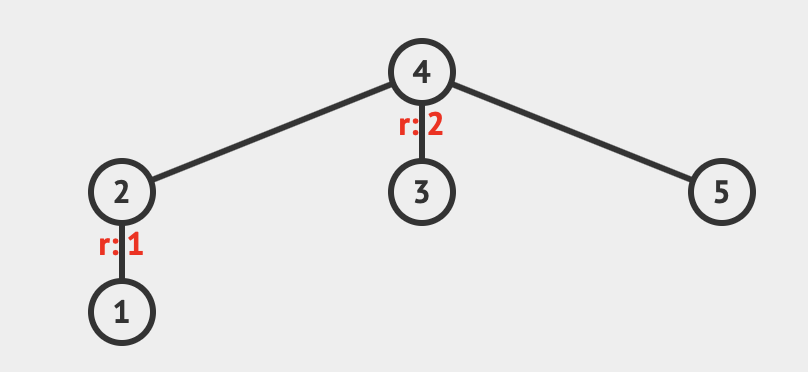
- 核心操作
// p[x]是x的集合编号,p[y]是y的集合编号
p[x] = y;
判断当前节点是否是树根
if (p[x] == x)
求节点的集合编号
while (p[x] != x)
x = p[x];
路径压缩优化,第一次求祖先节点的时候把所有遍历的点的父节点都设为祖先节点
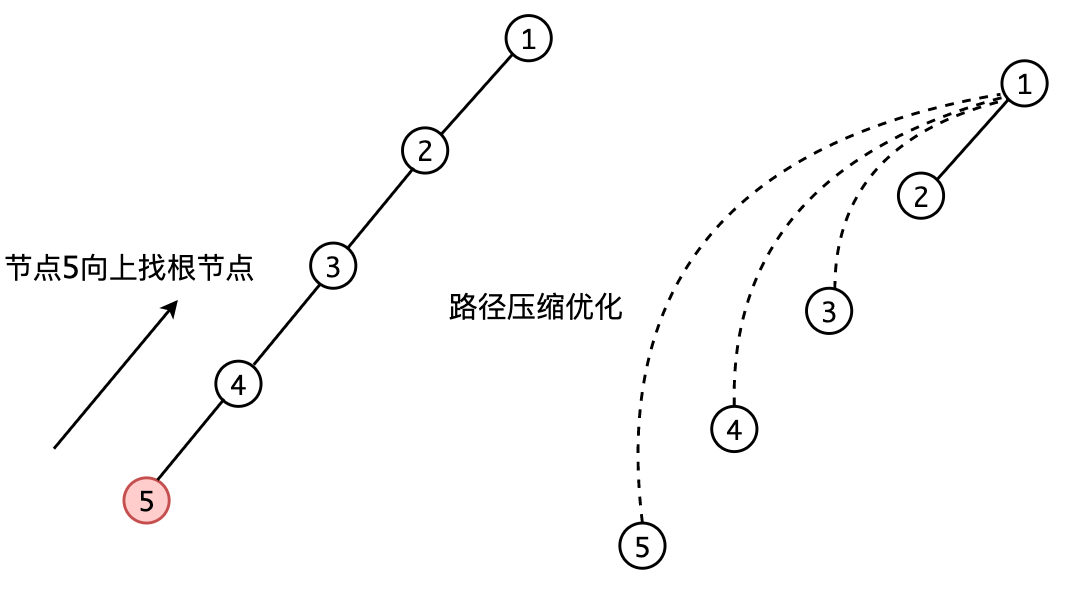
// 返回x的祖宗节点 + 路径压缩
int find (int x) {
if (p[x] != x)
p[x] = find(p[x]);
return p[x];
}
合并集合
一共有n个数,编号是1~n,最开始每个数各自在一个集合中。现在要进行m个操作,操作共有两种:
- “M a b”,将编号为a和b的两个数所在的集合合并,如果两个数已经在同一个集合中,则忽略这个操作;
- “Q a b”,询问编号为a和b的两个数是否在同一个集合中;
输入格式
第一行输入整数n和m。接下来m行,每行包含一个操作指令,指令为“M a b”或“Q a b”中的一种。
输出格式
对于每个询问指令”Q a b”,都要输出一个结果,如果a和b在同一集合内,则输出“Yes”,否则输出“No”。每个结果占一行。
数据范围
输入样例:
4 5
M 1 2
M 3 4
Q 1 2
Q 1 3
Q 3 4
输出样例:
Yes
No
Yes
#include <iostream>
using namespace std;
const int N = 100010;
int p[N];
int n, m;
// 核心find函数
int find(int x) {
if (x != p[x])
p[x] = find(p[x]);
return p[x];
}
int main() {
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; i++)
p[i] = i;
while (m--) {
char op[2];
int a, b;
scanf("%s%d%d", op, &a, &b);
if (op[0] == 'M')
p[find(a)] = find(b);
else {
if (find(a) != find(b))
printf("No\n");
else
printf("Yes\n");
}
}
return 0;
}
连通块中的数量
给定一个包含n个点(编号为1~n)的无向图,初始时图中没有边。现在要进行m个操作,操作共有三种:
- “C a b”,在点a和点b之间连一条边,a和b可能相等;
- “Q1 a b”,询问点a和点b是否在同一个连通块中,a和b可能相等;
- “Q2 a”,询问点a所在连通块中点的数量;
输入格式
第一行输入整数n和m。接下来m行,每行包含一个操作指令,指令为“C a b”,“Q1 a b”或“Q2 a”中的一种。
输出格式
对于每个询问指令”Q1 a b”,如果a和b在同一个连通块中,则输出“Yes”,否则输出“No”。
对于每个询问指令“Q2 a”,输出一个整数表示点a所在连通块中点的数量。每个结果占一行。
数据范围
输入样例:
5 5
C 1 2
Q1 1 2
Q2 1
C 2 5
Q2 5
输出样例:
Yes
2
3
#include <iostream>
#include <string>
using namespace std;
const int N = 100010;
// cnt数组维护连通块的结点数量
int p[N], cnt[N];
int n, m;
int find(int x) {
if (x != p[x])
p[x] = find(p[x]);
return p[x];
}
int main() {
cin >> n >> m;
// 初始化
for (int i = 1; i <= n; i++) {
p[i] = i;
cnt[i] = 1;
}
while (m--) {
string op;
int a, b;
cin >> op;
if (op == "C") {
cin >> a >> b;
a = find(a);
b = find(b);
if (a != b) {
p[a] = b;
// 注意这里不要写find(a)和find(b):因为上面合并之后,find(b)会变,所以我们在前面记录a和b
cnt[b] += cnt[a];
}
}
else if (op == "Q1") {
cin >> a >> b;
if (find(a) == find(b))
cout << "Yes" << endl;
else
cout << "No" << endl;
}
else {
cin >> a;
cout << cnt[find(a)] << endl;
}
}
return 0;
}
