基础篇部分和进阶篇部分介绍了树相关章节的基础知识和基础算法,本篇就PAT上相关习题做一个总结
DFS遍历相关
数叶子结点
家庭关系可以用家谱树来表示,给定一个家谱树,你的任务是找出其中没有孩子的成员。
输入格式
第一行包含一个整数 N 表示树中结点总数以及一个整数 M 表示非叶子结点数。
接下来 M 行,每行的格式为:
ID K ID[1] ID[2] ... ID[K]
ID 是一个两位数字,表示一个非叶子结点编号,K 是一个整数,表示它的子结点数,接下来的 K 个 ID[i] 也是两位数字,表示一个子结点的编号。
为了简单起见,我们将根结点固定设为 01。
所有结点的编号即为 01,02,03,…,31,32,33,…,N。
输出格式
输出从根结点开始,自上到下,树的每一层级分别包含多少个叶子节点。
输出占一行,整数之间用空格隔开。
数据范围
0<N<100
输入样例:
2 1
01 1 02
输出样例:
0 1
样例解释
该样例表示一棵只有 2 个结点的树,其中 01 结点是根,而 02 结点是其唯一的子节点。
因此,在根这一层级上,存在 0 个叶结点;在下一个级别上,有 1 个叶结点。
所以,我们应该在一行中输出0 1。
#include <iostream>
#include <vector>
using namespace std;
const int N = 110;
int n, m;
int cnt[N];
int max_depth;
vector<int> g[N];
/*
* DFS搜索,加上depth参数为了记录每一层的叶子结点个数
*/
void dfs(int u, int depth) {
// 说明u是叶子结点
if (g[u].size() == 0) {
cnt[depth]++;
max_depth = max(max_depth, depth);
return;
}
for (int i = 0; i < g[u].size(); i++) {
dfs(g[u][i], depth + 1);
}
}
int main() {
cin >> n >> m;
// 读入数据建树
for (int i = 0; i < m; i++) {
int id, k;
cin >> id >> k;
while(k--) {
int son;
cin >> son;
g[id].push_back(son);
}
}
dfs(1, 0);
cout << cnt[0];
for (int i = 1; i <= max_depth; i++) {
cout << " " << cnt[i];
}
cout << endl;
return 0;
}
完全二叉树
给定一个树,请你判断它是否是完全二叉树。
输入格式
第一行包含整数 N,表示树的结点个数。
树的结点编号为 0∼N−1。
接下来 N 行,每行对应一个结点,并给出该结点的左右子结点的编号,如果某个子结点不存在,则用 - 代替。
输出格式
如果是完全二叉树,则输出 YES 以及最后一个结点的编号。
如果不是,则输出 NO 以及根结点的编号。
数据范围
1≤N≤20
输入样例1:
9
7 8
- -
- -
- -
0 1
2 3
4 5
- -
- -
输出样例1:
YES 8
输入样例2:
8
- -
4 5
0 6
- -
2 3
- 7
- -
- -
输出样例2:
NO 1
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 30;
int n;
int l[N], r[N];
int level[N];
bool st[N];
int key, id;
// 判断是完全二叉树,我们根节点开始编号为1
void dfs(int root, int k) {
if (root == -1)
return;
if (key < k) {
key = k;
id = root;
}
// 左儿子 2 * k
dfs(l[root], k * 2);
// 右儿子 2 * k + 1
dfs(r[root], k * 2 + 1);
}
int main() {
cin >> n;
// 左右儿子全部先初始化为 -1
memset(l, -1, sizeof l);
memset(r, -1, sizeof r);
for (int i = 0; i < n; i++) {
string a, b;
cin >> a >> b;
if (a != "-") {
l[i] = stoi(a);
st[l[i]] = true;
}
if (b != "-") {
r[i] = stoi(b);
st[r[i]] = true;
}
}
// 不是任何结点的左右儿子就是根节点
int root = 0;
while(st[root])
root++;
dfs(root, 1);
// 全部按完全二叉树能填充进去,说明满足完全二叉树
if (key == n)
cout << "YES" << ' ' << id;
else
cout << "NO" << ' ' << root;
return 0;
}
等重路径
给定一个非空的树,树根为 R。
树中每个节点 Ti 的权重为 Wi。从 R 到 L 的路径权重定义为从根节点R 到任何叶节点L 的路径中包含的所有节点的权重之和。
现在给定一个加权树以及一个给定权重数字,请你找出树中所有的权重等于该数字的路径(必须从根节点到叶节点)。
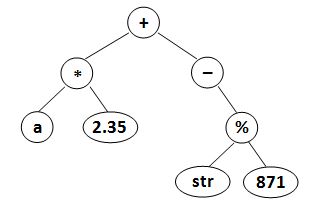
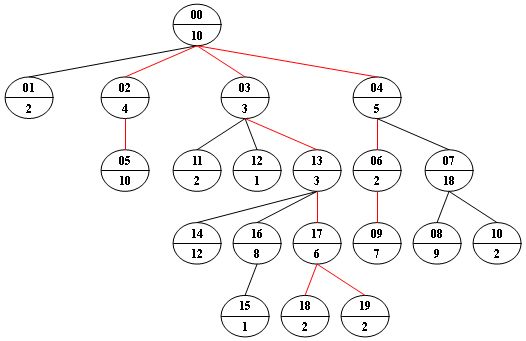
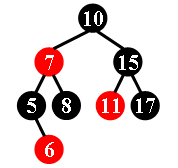
例如,我们考虑下图的树,对于每个节点,上方的数字是节点 ID,它是两位数字,而下方的数字是该节点的权重。
假设给定数为 24,则存在 4 个具有相同给定权重的不同路径:{10 5 2 7},{10 4 10},{10 3 3 6 2},{10 3 3 6 2}, 已经在图中用红色标出。
输入格式
第一行包含三个整数 N,M,S,分别表示树的总节点数量,非叶子节点数量,给定权重数字。
第二行包含 N 个整数 Wi,表示每个节点的权重。
接下来 M 行,每行的格式为:
ID K ID[1] ID[2] ... ID[K]
ID 是一个两位数字,表示一个非叶子结点编号,K 是一个整数,表示它的子结点数,接下来的 K 个 ID[i] 也是两位数字,表示一个子结点的编号。
出于方便考虑,根节点固定为 00,且树中所有节点的编号为 00∼N−1。
输出格式
以单调递减的顺序输出所有权重为S的路径。
每个路径占一行,从根节点到叶节点按顺序输出每个节点的权重。
注意:我们称 A 序列 {A1,A2,…,An} 大于 B 序列 {B1,B2,…,Bm},当且仅当存在一个整数 k,1≤k<min(n,m),对于所有 1≤i≤k,Ai=Bi 成立,并且 Ak+1>Bk+1。
数据范围
1≤N≤100,
0≤M<N,
0<S<230,
0<Wi<1000
输入样例:
20 9 24
10 2 4 3 5 10 2 18 9 7 2 2 1 3 12 1 8 6 2 2
00 4 01 02 03 04
02 1 05
04 2 06 07
03 3 11 12 13
06 1 09
07 2 08 10
16 1 15
13 3 14 16 17
17 2 18 19
输出样例:
10 5 2 7
10 4 10
10 3 3 6 2
10 3 3 6 2
- 计算所有叶结点到根节点路径权值和
- 等于目标值,存下来
- vctor排序,默认字典序
#include <iostream>
#include <cstring>
#include <vector>
#include <algorithm>
using namespace std;
const int N = 110;
int n, m, S;
int w[N];
bool g[N][N];
vector<vector<int>> res;
void dfs(int u, int s, vector<int>& path) {
bool is_leaf = true;
// 判断是否为叶子节点
for (int i = 0; i < n; i++) {
if (g[u][i]) {
is_leaf = false;
break;
}
}
// 是叶子结点
if (is_leaf) {
// 权值等于目标权值S
if (s == S)
res.push_back(path);
}
else {
for (int i = 0; i < n; i++) {
if (g[u][i]) {
path.push_back(w[i]);
dfs(i, s + w[i], path);
// 恢复现场
path.pop_back();
}
}
}
}
int main() {
cin >> n >> m >> S;
for (int i = 0; i < n; i++)
cin >> w[i];
while (m--) {
int id, k;
cin >> id >> k;
while (k--) {
int son;
cin >> son;
g[id][son] = true;
}
}
vector<int> path({w[0]});
// 从根节点开始搜
dfs(0, w[0], path);
sort(res.begin(), res.end(), greater<vector<int>>());
for (auto a : res) {
cout << a[0];
for (int i = 1; i < a.size(); i++)
cout << ' ' << a[i];
cout << endl;
}
return 0;
}
供应链总销售额
供应链是由零售商,经销商和供应商构成的销售网络,每个人都参与将产品从供应商转移到客户的过程。
整个销售网络可以看作一个树形结构,从根部的供应商往下,每个人从上一级供应商中买入商品后,假定买入价格为 P,则会以高出买入价 r% 的价格向下出售。
只有零售商(即叶节点)可以直接将产品销售给顾客。
现在,给定整个销售网络,请你计算所有零售商的总销售额。
输入格式
第一行包含三个数,N 表示供应链总成员数(所有成员编号从 0 到 N−1,根部供应商编号为 0),P 表示根部供应商的每件产品的售卖价格,r,溢价百分比。
接下来 N 行,每行包含一个成员的信息,格式如下:
Ki ID[1] ID[2] … ID[Ki]
其中第 i 行,Ki 表示从供应商 i 直接进货的成员数,接下来 Ki 个整数是每个进货成员的编号。
如果某一行的 Kj 为 0,则表示这是零售商,那么后面只会跟一个数字,表示卖给客户的产品总件数。
输出格式
输出总销售额,保留一位小数。
数据范围
1≤N≤105,
0<P≤1000,
0<r≤50
每个零售商手中的产品不超过 100 件。
最终答案保证不超过 1010。
输入样例:
10 1.80 1.00
3 2 3 5
1 9
1 4
1 7
0 7
2 6 1
1 8
0 9
0 4
0 3
输出样例:
42.4
- 问题的本质是求叶子结点的层数
记忆化搜索
求各个结点到根节点的距离:存储节点的时候,只存储每个结点的父节点信息
#include <iostream>
#include <cstring>
#include <algorithm>
#include <cmath>
using namespace std;
const int N = 100010;
int n;
double P, R;
// 存所有节点
int p[N];
int f[N];
// 记录销售量
int c[N];
// 记忆化搜索过程,求每个结点到根节点的距离
int dfs(int u) {
// f[u]已经被计算出来,直接返回
if (f[u] != -1)
return f[u];
// 根节点
if (p[u] == -1) {
f[u] = 0;
return 0;
}
// 当前结点层数 = 父节点层数 + 1
f[u] = dfs(p[u]) + 1;
return f[u];
}
int main() {
cin >> n >> P >> R;
memset(p, -1, sizeof p);
for (int i = 0; i < n; i++) {
int k;
cin >> k;
for (int j = 0; j < k; j++) {
int son;
cin >> son;
p[son] = i;
}
// 节点是叶子节点,输入销售量
if (k == 0) {
cin >> c[i];
}
}
memset(f, -1, sizeof f);
double res = 0;
for (int i = 0; i < n; i++) {
if (c[i] != 0)
res += c[i] * P * pow(1 + R / 100, dfs(i));
}
printf("%.1lf\n", res);
return 0;
}
DFS解法
#include <iostream>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <vector>
#include <unordered_map>
using namespace std;
const int N = 100010;
int n;
double P, R;
// 记录销售量
int c[N];
// 使用邻接表来存树
vector<int> g[N];
double total = 0;
// 返回节点到根节点的距离
void dfs(int u, double p) {
if (c[u] > 0) {
total += c[u] * p;
}
else {
for (int i = 0; i < g[u].size(); i++) {
dfs(g[u][i], p * (1 + R / 100.0));
}
}
}
int main() {
cin >> n >> P >> R;
for (int i = 0; i < n; i++) {
int k;
cin >> k;
for (int j = 0; j < k; j++) {
int son;
cin >> son;
g[i].push_back(son);
}
// 节点是叶子节点,输入销售量
if (k == 0) {
cin >> c[i];
}
}
dfs(0, P);
printf("%.1lf\n", total);
return 0;
}
供应链最高价格
供应链是由零售商,经销商和供应商构成的销售网络,每个人都参与将产品从供应商转移到客户的过程。
整个销售网络可以看作一个树形结构,从根部的供应商往下,每个人从上一级供应商中买入商品后,假定买入价格为 P,则会以高出买入价 r% 的价格向下出售。
只有零售商(即叶节点)可以直接将产品销售给顾客。
现在,给定整个销售网络,请你计算零售商能达到的最高销售价格。
输入格式
第一行包含三个数,N 表示供应链总成员数(所有成员编号为 0 到 N−1);P 表示根部供应商的产品销售价格;r,表示溢价百分比。
第二行包含 N 个数字,第 i 个数字 Si 是编号为 i 的成员的上级供应商的编号。根部供应商的 Sroot 为 -1。
输出格式
输出零售商可达到的最高销售价格,保留两位小数,以及可达到最高销售价格的零售商的数量。
数据范围
1≤N≤105,
0<P≤1000,
0<r≤50,
最终答案保证不超过 1010。
输入样例:
9 1.80 1.00
1 5 4 4 -1 4 5 3 6
输出样例:
1.85 2
- 问题本质是求最大深度
#include <iostream>
#include <vector>
#include <cmath>
using namespace std;
const int N = 100010;
int n;
double P, R;
vector<int> g[N];
int max_depth = 0;
int cnt = 0;
void dfs(int u, int depth) {
if (g[u].size() == 0) {
if (depth > max_depth) {
max_depth = depth;
cnt = 1;
}
else if (depth == max_depth)
cnt++;
return;
}
else {
for (int i = 0; i < g[u].size(); i++)
dfs(g[u][i], depth + 1);
}
}
int main() {
cin >> n >> P >> R;
int root;
for (int i = 0; i < n; i++) {
int a;
cin >> a;
if (a != -1)
g[a].push_back(i);
else {
root = i;
}
}
dfs(root, 0);
printf("%.2lf %d\n", P * pow(1 + R / 100, max_depth), cnt);
return 0;
}
供应链最低价格
供应链是由零售商,经销商和供应商构成的销售网络,每个人都参与将产品从供应商转移到客户的过程。
整个销售网络可以看作一个树形结构,从根部的供应商往下,每个人从上一级供应商中买入商品后,假定买入价格为 P,则会以高出买入价 r% 的价格向下出售。
只有零售商(即叶节点)可以直接将产品销售给顾客。
现在,给定整个销售网络,请你计算零售商能达到的最低销售价格。
输入格式
第一行包含三个数,N 表示供应链总成员数(所有成员编号从 0 到 N−1,根部供应商编号为 0),P 表示根部供应商的产品售卖价格,r,溢价百分比。
接下来 N 行,每行包含一个成员的信息,格式如下:
Ki ID[1] ID[2] … ID[Ki]
其中第 i 行,Ki 表示从供应商 i 直接进货的成员数,接下来 Ki 个整数是每个进货成员的编号。
如果 Kj 为 0 则表示第 j 名成员是零售商。
输出格式
输出零售商可达到的最低销售价格,保留四位小数,以及可达到最低销售价格的零售商的数量。
数据范围
1≤N≤105,
0<P≤1000,
0<r≤50,
最终答案保证不超过 1010
输入样例:
10 1.80 1.00
3 2 3 5
1 9
1 4
1 7
0
2 6 1
1 8
0
0
0
输出样例:
1.8362 2
- 问题本质是求最低深度
#include <iostream>
#include <vector>
#include <cmath>
using namespace std;
const int N = 100010;
int n;
double P, R;
vector<int> g[N];
int min_depth = -1;
int cnt;
void dfs (int u, int depth) {
if (g[u].size() == 0) {
if (depth < min_depth || min_depth == -1) {
min_depth = depth;
cnt = 1;
}
else if (depth == min_depth)
cnt++;
}
else {
for (int i = 0; i < g[u].size(); i++)
dfs(g[u][i], depth + 1);
}
}
int main() {
cin >> n >> P >> R;
for (int i = 0; i < n; i++) {
int k;
cin >> k;
while (k--) {
int a;
cin >> a;
g[i].push_back(a);
}
}
dfs(0, 0);
printf("%.4lf %d\n", P * pow(1 + R / 100.0, min_depth), cnt);
return 0;
}
堆路径
在计算机科学中,堆是一种的基于树的专用数据结构,它具有堆属性:
如果 P 是 C 的父结点,则在大顶堆中 P 结点的权值大于或等于 C 结点的权值,在小顶堆中 P 结点的权值小于或等于 C 结点的权值。
一种堆的常见实现是二叉堆,它是由完全二叉树来实现的。
可以肯定的是,在大顶/小顶堆中,任何从根到叶子的路径都必须按非递增/非递减顺序排列。
你的任务是检查给定完全二叉树中的每个路径,以判断它是否是堆。
输入格式
第一行包含整数 N,表示树中结点数量。
第二行包含 N 个 不同 的整数,表示给定完全二叉树的层序遍历序列。
输出格式
对于给定的树,首先输出所有从根到叶子的路径。
每条路径占一行,数字之间用空格隔开,行首行尾不得有多余空格。
必须以如下顺序输出路径:对于树中的每个结点都必须满足,其右子树中的路径先于其左子树中的路径输出。
最后一行,如果是大顶堆,则输出 Max Heap,如果是小顶堆,则输出 Min Heap,如果不是堆,则输出 Not Heap。
数据范围
1<N≤1000
输入样例1:
8
98 72 86 60 65 12 23 50
输出样例1:
98 86 23
98 86 12
98 72 65
98 72 60 50
Max Heap
输入样例2:
8
8 38 25 58 52 82 70 60
输出样例2:
8 25 70
8 25 82
8 38 52
8 38 58 60
Min Heap
输入样例3:
8
10 28 15 12 34 9 8 56
输出样例3:
10 15 8
10 15 9
10 28 34
10 28 12 56
Not Heap
-
大顶堆:从根节点往下路径严格下降
-
小顶堆:从根节点往上路径严格上升
-
DFS搜到所有路径,进行判断是否满足大顶堆或小顶堆
#include <iostream>
#include <vector>
using namespace std;
const int N = 1010;
int n;
vector<vector<int>> res;
int h[N];
bool min_heap, max_heap;
void dfs(int u, vector<int>& path) {
path.push_back(h[u]);
// 是叶子结点的情况
if (2 * u > n) {
res.push_back(path);
}
if (2 * u + 1 <= n)
dfs(2 * u + 1, path);
if (2 * u <= n)
dfs(2 * u, path);
path.pop_back();
}
int main() {
cin >> n;
for (int i = 1; i <= n; i++) {
cin >> h[i];
}
vector<int> path;
dfs(1, path);
for (auto p : res) {
cout << p[0];
for (int i = 1; i < p.size(); i++) {
cout << ' ' << p[i];
if (p[i] > p[i - 1])
min_heap = true;
else if (p[i] < p[i - 1])
max_heap = true;
}
cout << endl;
}
if (min_heap && max_heap)
cout << "Not Heap" << endl;
else if (min_heap)
cout << "Min Heap" << endl;
else
cout << "Max Heap" << endl;
return 0;
}
中缀表达式
给定一个句法二叉树,请你输出相应的中缀表达式,并利用括号反映运算符的优先级。
输入格式
第一行包含整数 N 表示二叉树的总结点个数。
接下来 N 行,每行以下列格式给出一个结点的信息(第 i 行对应于第 i 个结点):
data left_child right_child
其中 data 是一个长度不超过 10 的字符串,left_child 和 right_child 分别是该结点的左右子结点编号。
所有结点编号从 1 到 N,NULL 用 -1 表示。
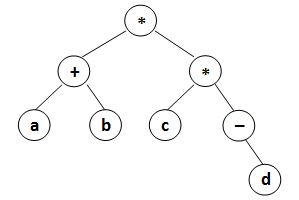
以下两个图分别对应样例 1 和样例 2。
输出格式
请在一行输出中缀表达式,并利用括号反映运算符的优先级。
注意,不能有多余括号,请任何符号之间不得有空格。
数据范围
1≤N≤20
输入样例1:
8
* 8 7
a -1 -1
* 4 1
+ 2 5
b -1 -1
d -1 -1
- -1 6
c -1 -1
输出样例1:
(a+b)*(c*(-d))
输入样例2:
8
2.35 -1 -1
* 6 1
- -1 4
% 7 8
+ 2 3
a -1 -1
str -1 -1
871 -1 -1
输出样例2:
(a*2.35)+(-(str%871))
- 中序遍历序列加括号的一个过程(注意叶子结点不用添加括号)
#include <iostream>
#include <string>
using namespace std;
const int N = 30;
int n;
string w[N];
int l[N], r[N];
bool st[N], is_leaf[N];
string dfs (int u) {
string left, right;
if (l[u] != -1) {
left = dfs(l[u]);
// 判断当前层加不加括号
if (!is_leaf[l[u]])
left = "(" + left + ")";
}
if (r[u] != -1) {
right = dfs(r[u]);
if (!is_leaf[r[u]])
right = "(" + right + ")";
}
return left + w[u] + right;
}
int main() {
cin >> n;
for (int i = 1; i <= n; i++) {
cin >> w[i] >> l[i] >> r[i];
// 如果是根节点,节点编号一定不是左右儿子所出现的编号
if (l[i])
st[l[i]] = true;
if (r[i])
st[r[i]] = true;
// 标记是否是叶子节点,叶子节点不用添加左右括号
if (l[i] == -1 && r[i] == -1)
is_leaf[i] = true;
}
// 找到根节点编号
int root = 1;
while (st[root])
root++;
cout << dfs(root) << endl;
return 0;
}
BFS遍历相关
树的遍历
一个二叉树,树中每个节点的权值互不相同。
现在给出它的后序遍历和中序遍历,请你输出它的层序遍历。
输入格式
第一行包含整数 N,表示二叉树的节点数。
第二行包含 N 个整数,表示二叉树的后序遍历。
第三行包含 N 个整数,表示二叉树的中序遍历。
输出格式
输出一行 N 个整数,表示二叉树的层序遍历。
数据范围
1≤N≤30
输入样例:
7
2 3 1 5 7 6 4
1 2 3 4 5 6 7
输出样例:
4 1 6 3 5 7 2
#include <iostream>
#include <unordered_map>
#include <algorithm>
#include <cstring>
#include <queue>
using namespace std;
const int N = 40;
// 存储后序和中序的序列
int post[N], in[N];
// 用哈希表存根节点的左子树和右子树:第一维为表示树结点的值 第二维表示树节点指向的节点
unordered_map<int, int> l, r;
// 记录中序序列的下标
unordered_map<int, int> pos;
// 中序+后序重建二叉树
int build(int is, int ie, int ps, int pe) {
// 找到根节点
int root = post[pe];
// 找到根节点在中序序列中的位置
int k = pos[root];
// 左子树存在,构建左子树
if (is < k)
l[root] = build(is, k - 1, ps, ps + (k - 1 - is));
// 右子树存在,构建右子树
if (k < ie)
r[root] = build(k + 1, ie, ps + (k - 1 - is) + 1, pe - 1);
return root;
}
// 二叉树广度优先搜索,使用队列
void bfs(int root) {
queue<int> qu;
vector<int> res;
qu.push(root);
while (!qu.empty()) {
int t = qu.front();
qu.pop();
res.push_back(t);
if (l.count(t))
qu.push(l[t]);
if (r.count(t))
qu.push(r[t]);
}
cout << res[0];
for (int i = 1; i < res.size(); i++)
cout << ' ' << res[i];
}
int main() {
int n;
cin >> n;
for (int i = 0; i < n; i++) {
cin >> post[i];
}
// 读入中序序列并保存中序序列的下标
for (int i = 0; i < n; i++) {
cin >> in[i];
pos[in[i]] = i;
}
// 构建树
int root = build(0, n - 1, 0, n - 1);
bfs(root);
}
Z字型遍历二叉树
假设一个二叉树上各结点的权值互不相同。
我们就可以通过其后序遍历和中序遍历来确定唯一二叉树。
请你输出该二叉树的 Z 字形遍历序列----也就是说,从根结点开始,逐层遍历,第一层从右到左遍历,第二层从左到右遍历,第三层从右到左遍历,以此类推。
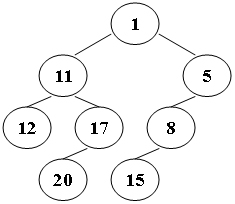
例如,下图所示二叉树,其 Z 字形遍历序列应该为:1 11 5 8 17 12 20 15。
输入格式
第一行包含整数 N,表示二叉树结点数量。
第二行包含 N 个整数,表示二叉树的中序遍历序列。
第三行包含 N 个整数,表示二叉树的后序遍历序列。
输出格式
输出二叉树的 Z 字形遍历序列。
数据范围
1≤N≤30
输入样例:
8
12 11 20 17 1 15 8 5
12 20 17 11 15 8 5 1
输出样例:
1 11 5 8 17 12 20 15
#include <iostream>
#include <algorithm>
#include <unordered_map>
#include <queue>
#include <vector>
using namespace std;
const int N = 40;
vector<int> res;
int n;
unordered_map<int, int> l, r, pos;
int in[N], post[N];
// 构建二叉树
int build (int il, int ir, int pl, int pr) {
int root = post[pr];
int k = pos[root];
if (il < k)
l[root] = build(il, k - 1, pl, pl + k - il - 1);
if (ir > k)
r[root] = build(k + 1, ir, pl + k - il - 1 + 1, pr - 1);
return root;
}
// 层序遍历
void bfs (int u) {
queue<int> q;
q.push(u);
int step = 0;
while (!q.empty()) {
vector<int> v;
int cnt = q.size();
while (cnt--) {
int t = q.front();
q.pop();
v.push_back(t);
if (l.count(t))
q.push(l[t]);
if (r.count(t))
q.push(r[t]);
}
if (++step % 2)
reverse(v.begin(), v.end());
for (int i = 0; i < v.size(); i++)
res.push_back(v[i]);
}
}
int main() {
cin >> n;
// 使用hash记录下中序遍历的下标位置
for (int i = 0; i < n; i++) {
cin >> in[i];
pos[in[i]] = i;
}
for (int i = 0; i < n; i++) {
cin >> post[i];
}
int root = build(0, n - 1, 0, n - 1);
bfs(root);
cout << res[0];
for (int i = 1; i < res.size(); i++)
cout << ' ' << res[i];
return 0;
}
最大的一代
家庭关系可以用家谱树来表示,同一层上的所有结点都属于同一代人。
请你找出人数最多的一代。
输入格式
第一行包含一个整数 N 表示树中结点总数以及一个整数 M 表示非叶子结点数。
接下来 M 行,每行的格式为:
ID K ID[1] ID[2] ... ID[K]
ID 是一个两位数字,表示一个非叶子结点编号,K 是一个整数,表示它的子结点数,接下来的 K 个 ID[i] 也是两位数字,表示一个子结点的编号。
为了简单起见,我们将根结点固定设为 01。
所有结点的编号即为 01,02,03,…,31,32,33,…,N。
输出格式
输出结点数量最多的一层的结点数量以及层级。
保证答案唯一。
根结点定义为第一层。
数据范围
0<N<100
输入样例:
23 13
21 1 23
01 4 03 02 04 05
03 3 06 07 08
06 2 12 13
13 1 21
08 2 15 16
02 2 09 10
11 2 19 20
17 1 22
05 1 11
07 1 14
09 1 17
10 1 18
输出样例:
9 4
- BFS的时候存下每一层的结点,然后找到最大的那一层输出
#include <iostream>
#include <queue>
#include <vector>
using namespace std;
const int N = 110;
int n, m;
bool g[N][N];
vector<vector<int>> level;
void bfs(int u) {
queue<int> q;
q.push(u);
while (!q.empty()) {
int cnt = q.size();
vector<int> res;
while (cnt--) {
int t = q.front();
res.push_back(t);
q.pop();
for (int i = 1; i <= n; i++) {
if (g[t][i])
q.push(i);
}
}
level.push_back(res);
}
}
int main() {
cin >> n >> m;
while (m--) {
int id, k;
cin >> id >> k;
while (k--) {
int son;
cin >> son;
g[id][son] = true;
}
}
bfs(1);
int max_size = 0;
int max_id;
for (int i = 0; i < level.size(); i++) {
if (level[i].size() > max_size) {
max_id = i;
max_size = level[i].size();
}
}
cout << level[max_id].size() << ' ' << max_id + 1 << endl;
return 0;
}
二叉搜索树
判断前序序列能否构成二叉搜索树(镜像)
二叉搜索树 (BST) 递归定义为具有以下属性的二叉树:
- 若它的左子树不空,则左子树上所有结点的值均小于它的根结点的值
- 若它的右子树不空,则右子树上所有结点的值均大于或等于它的根结点的值
- 它的左、右子树也分别为二叉搜索树
我们将二叉搜索树镜面翻转得到的树称为二叉搜索树的镜像。
现在,给定一个整数序列,请你判断它是否可能是某个二叉搜索树或其镜像进行前序遍历的结果。
输入格式
第一行包含整数 N,表示节点数量。
第二行包含 N 个整数。
输出格式
如果给定整数序列是某个二叉搜索树或其镜像的前序遍历序列,则在第一行输出 YES,否则输出 NO。
如果你的答案是 YES,则还需要在第二行输出这棵树的后序遍历序列。
数据范围
1≤N≤1000
输入样例1:
7
8 6 5 7 10 8 11
输出样例1:
YES
5 7 6 8 11 10 8
输入样例2:
7
8 10 11 8 6 7 5
输出样例2:
YES
11 8 10 7 5 6 8
输入样例3:
7
8 6 8 5 10 9 11
输出样例3:
NO
- 左子树要严格小于左子树,右子树大于等于左子树,所以当出现相同权值结点的时候,我们要取中序序列中相同值是第一个的位置
- 镜像之后的中序序列是从大到小,每次在中序序列中找最后一个出现相同值的位置,刚好和镜像之前相反
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 1010;
int n, cnt;
int preorder[N], inorder[N], postorder[N];
bool build (int il, int ir, int pl, int pr, int type) {
// 当所有点都用完,可以构建成功
if (il > ir)
return true;
int root = preorder[pl];
int k;
// 正向
if (type == 0) {
// 找到第一个相等的节点(BST定义)
for (k = il; k <= ir; k++) {
if (inorder[k] == root)
break;
}
// 找不到构建失败
if (k > ir)
return false;
}
else {
// 反向找到第一个相等的节点(BST定义)
for (k = ir; k >= il; k--) {
if (inorder[k] == root)
break;
}
if (k < il)
return false;
}
bool res = true;
if (!build(il, k - 1, pl + 1, pl + 1 + (k - 1 - il), type))
res = false;
if (!build(k + 1, ir, pl + 1 + (k - 1 - il) + 1, pr, type))
res = false;
postorder[cnt++] = root;
return res;
}
int main() {
cin >> n;
for(int i = 0; i < n; i++) {
cin >> preorder[i];
inorder[i] = preorder[i];
}
sort(inorder, inorder + n);
// 正常建树是否可以建成功
if (build(0, n - 1, 0, n - 1, 0)) {
cout << "YES" << endl;
cout << postorder[0];
for (int i = 1; i < n; i++)
cout << ' ' << postorder[i];
cout << endl;
}else{
reverse(inorder, inorder + n);
// 判断镜像建树是否可以建成功
cnt = 0;
if (build(0, n - 1, 0, n - 1, 1)) {
cout << "YES" << endl;
cout << postorder[0];
for (int i = 1; i < n; i++)
cout << ' ' << postorder[i];
cout << endl;
}else
cout << "NO" << endl;
}
return 0;
}
判断完全二叉搜索树
二叉搜索树 (BST) 递归定义为具有以下属性的二叉树:
- 若它的左子树不空,则左子树上所有结点的值均小于它的根结点的值
- 若它的右子树不空,则右子树上所有结点的值均大于或等于它的根结点的值
- 它的左、右子树也分别为二叉搜索树
完全二叉树 (CBT) 定义为除最深层外的其他层的结点数都达到最大个数,最深层的所有结点都连续集中在最左边的二叉树。
现在,给定 N 个不同非负整数,表示 N 个结点的权值,用这 N 个结点可以构成唯一的完全二叉搜索树。
请你输出该完全二叉搜索树的层序遍历。
输入格式
第一行包含整数 N,表示结点个数。
第二行包含 N 个不同非负整数,表示每个结点的权值。
输出格式
共一行,输出给定完全二叉搜索树的层序遍历序列。
数据范围
1≤N≤1000,
结点权值不超过 2000。
输入样例:
10
1 2 3 4 5 6 7 8 9 0
输出样例:
6 3 8 1 5 7 9 0 2 4
- 完全二叉树当前结点编号x,左儿子2 * x,右儿子2 * x + 1,父节点 x / 2
- 构建n个结点的完全二叉树
- 当使用中序序列填进完全二叉树,使其满足二叉搜索树的性质
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1010;
int n;
int w[N], t[N];
// 将中序遍历填进完全二叉树使其满足完全二叉搜索树性质
int dfs(int u, int& k) {
if (u * 2 <= n)
dfs(u * 2, k);
t[u] = w[k++];
if (u * 2 + 1 <= n)
dfs(u * 2 + 1, k);
}
int main() {
cin >> n;
for (int i = 0; i < n; i++) {
cin >> w[i];
}
// 排完序后w中存的就是中序遍历
sort(w, w + n);
int k = 0;
dfs(1, k);
cout << t[1];
for (int i = 2; i <= n; i++)
cout << ' ' << t[i];
return 0;
}
构建二叉搜索树(输入为左右儿子)
二叉搜索树 (BST) 递归定义为具有以下属性的二叉树:
- 若它的左子树不空,则左子树上所有结点的值均小于它的根结点的值
- 若它的右子树不空,则右子树上所有结点的值均大于或等于它的根结点的值
- 它的左、右子树也分别为二叉搜索树
给定二叉树的具体结构以及一系列不同的整数,只有一种方法可以将这些数填充到树中,以使结果树满足 BST 的定义。
请你输出结果树的层序遍历。
示例如图 1 和图 2 所示。
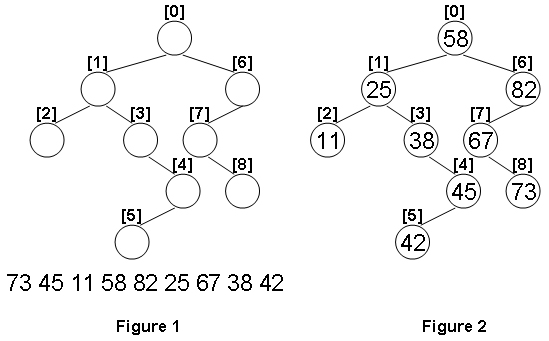
输入格式
第一行包含一个正整数 N,表示树的结点个数。
所有结点的编号为 0∼N−1,并且编号为 0 的结点是根结点。
接下来 N 行,第 i 行(从 0 计数)包含结点 i 的左右子结点编号。如果该结点的某个子结点不存在,则用 −1 表示。
最后一行,包含 N 个不同的整数,表示要插入树中的数值。
输出格式
输出结果树的层序遍历序列。
数据范围
1≤N≤100
输入样例:
9
1 6
2 3
-1 -1
-1 4
5 -1
-1 -1
7 -1
-1 8
-1 -1
73 45 11 58 82 25 67 38 42
输出样例:
58 25 82 11 38 67 45 73 42
#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue>
using namespace std;
const int N = 110;
int n, cnt;
// 存左右儿子
int l[N], r[N];
int a[N];
// 存节点权值
int w[N];
int p[N];
// 中序遍历去填充节点
void dfs(int u, int& k) {
if (u == -1)
return;
dfs(l[u], k);
w[u] = a[k++];
dfs(r[u], k);
}
// 得到节点编号的层次遍历结果p
void bfs() {
queue<int> q;
q.push(0);
while (!q.empty()) {
int t = q.front();
p[cnt++] = t;
q.pop();
if (l[t] != -1)
q.push(l[t]);
if (r[t] != -1)
q.push(r[t]);
}
}
int main() {
cin >> n;
for (int i = 0; i < n; i++){
cin >> l[i] >> r[i];
}
for (int i = 0; i < n; i++) {
cin >> a[i];
}
sort(a, a + n);
int k = 0;
dfs(0, k);
bfs();
cout << w[p[0]];
for (int i = 1; i < n; i++) {
cout << ' ' << w[p[i]];
}
cout << endl;
return 0;
}
二叉搜索树最后两层结点数量(根据插入序列建BST)
二叉搜索树 (BST) 递归定义为具有以下属性的二叉树:
- 若它的左子树不空,则左子树上所有结点的值均小于或等于它的根结点的值
- 若它的右子树不空,则右子树上所有结点的值均大于它的根结点的值
- 它的左、右子树也分别为二叉搜索树
将一系列数字按顺序插入到一个空的二叉搜索树中,然后,请你计算结果树的最低两层的结点个数。
输入格式
第一行包含整数 N,表示插入数字序列包含的数字个数。
第二行包含 N 个整数,表示插入数字序列。
输出格式
以如下格式,在一行中,输出结果树的最后两层的结点数:
n1 + n2 = n
n1 是最底层结点数量,n2 是倒数第二层结点数量,n 是它们的和。
数据范围
1≤N≤1000,
−1000≤ 插入数字 ≤1000。
输入样例:
9
25 30 42 16 20 20 35 -5 28
输出样例:
2 + 4 = 6
#include <iostream>
using namespace std;
const int N = 1010;
int n;
int l[N], r[N];
// 记录结点权值
int v[N];
int max_depth, idx;
int cnt[N];
// 不断插入节点生成二叉搜索树(递归)
void insert (int& u, int w) {
// 现在就要进行插入
if (u == 0) {
u = ++idx;
v[u] = w;
}
// 插入到左子树
else if (w <= v[u])
insert(l[u], w);
else
insert(r[u], w);
}
void dfs (int u, int depth) {
if (u == 0)
return;
// 记录当前层节点数
cnt[depth]++;
max_depth = max(max_depth, depth);
dfs(l[u], depth + 1);
dfs(r[u], depth + 1);
}
int main () {
cin >> n;
int root = 0;
for (int i = 0; i < n; i++) {
int a;
cin >> a;
insert(root, a);
}
// dfs遍历树
dfs(root, 0);
cout << cnt[max_depth] << " + " << cnt[max_depth - 1] << " = " << cnt[max_depth - 1] + cnt[max_depth] << endl;
return 0;
}
通过序列构建树
使用序列构建二叉树的题目出现频次较多,代码模板要熟记在心
再次树遍历
通过使用栈可以以非递归方式实现二叉树的中序遍历。
例如,假设遍历一个如下图所示的 6 节点的二叉树(节点编号从 1 到 6)。
则堆栈操作为:push(1); push(2); push(3); pop(); pop(); push(4); pop(); pop(); push(5); push(6); pop(); pop()。
我们可以从此操作序列中生成唯一的二叉树。
你的任务是给出这棵树的后序遍历。
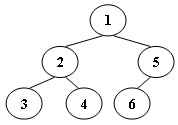
输入格式
第一行包含整数 N,表示树中节点个数。
树中节点编号从 1 到 N。
接下来 2N 行,每行包含一个栈操作,格式为:
Push X,将编号为 X 的节点压入栈中。Pop,弹出栈顶元素。
输出格式
输出这个二叉树的后序遍历序列。
数据保证有解,数和数之间用空格隔开,末尾不能有多余空格。
数据范围
1≤N≤30
输入样例:
6
Push 1
Push 2
Push 3
Pop
Pop
Push 4
Pop
Pop
Push 5
Push 6
Pop
Pop
输出样例:
3 4 2 6 5 1
- Push操作序列顺序就是前序遍历
- Pop出的序列是中序序列
#include <iostream>
#include <algorithm>
#include <stack>
#include <string>
using namespace std;
const int N = 40;
int pre[N], in[N], post[N];
int n, cnt;
void build (int pl, int pr, int il, int ir) {
if (il > ir)
return;
int root = pre[pl];
// 中序序列中找到根的位置
int k;
for (k = il; k <= ir; k++) {
if (in[k] == root)
break;
}
build (pl + 1, pl + 1 + (k - 1 - il), il, k - 1);
build (pl + 1 + (k - 1 - il) + 1, pr, k + 1, ir);
post[cnt++] = root;
}
int main() {
cin >> n;
stack<int> s;
int kp = 0;
int ki = 0;
for (int i = 0; i < n * 2; i++) {
string op;
cin >> op;
if (op == "Push") {
int a;
cin >> a;
pre[kp++] = a;
s.push(a);
}
else {
in[ki++] = s.top();
s.pop();
}
}
build(0, n - 1, 0, n - 1);
cout << post[0];
for (int i = 1; i < n; i++) {
cout << ' ' << post[i];
}
cout << endl;
return 0;
}
反转二叉树
以下是来自 Max Howell @twitter 的内容:
谷歌:我们的百分之九十的工程师都使用你编写的软件,但是你连在白板上反转二叉树都做不到,还是滚吧。
现在,请你证明你会反转二叉树。
输入格式
第一行包含一个整数 N,表示树的结点数量。
所有结点编号从 0 到 N−1。
接下来 N 行,每行对应一个 0∼N−1 的结点,给出该结点的左右子结点的编号,如果该结点的某个子结点不存在,则用 − 表示。
输出格式
输出反转后二叉树的层序遍历序列和中序遍历序列,每个序列占一行。
相邻数字之间用空格隔开,末尾不得有多余空格。
数据范围
1≤N≤10
输入样例:
8
1 -
- -
0 -
2 7
- -
- -
5 -
4 6
输出样例:
3 7 2 6 4 0 5 1
6 5 7 4 3 2 0 1
#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue>
using namespace std;
const int N = 20;
int n, cnt;
// 记录左儿子和右儿子
int l[N], r[N];
// 记录中序遍历和层序遍历
int in[N], level[N];
bool st[N];
// 翻转二叉树
void reverse(int root) {
if (root == -1)
return;
reverse(l[root]);
reverse(r[root]);
swap(l[root], r[root]);
}
void bfs(int root) {
queue<int> q;
q.push(root);
while(!q.empty()){
int t = q.front();
level[cnt++] = t;
q.pop();
if (l[t] != -1)
q.push(l[t]);
if (r[t] != -1)
q.push(r[t]);
}
cout << level[0];
for (int i = 1; i < n; i++) {
cout << ' ' << level[i];
}
}
void dfs(int root) {
if (root == -1)
return;
dfs(l[root]);
in[cnt++] = root;
dfs(r[root]);
}
int main() {
cin >> n;
memset(l, -1, sizeof l);
memset(r, -1, sizeof r);
for (int i = 0; i < n; i++) {
string a, b;
cin >> a;
if (a != "-"){
l[i] = stoi(a);
st[l[i]] = true;
}
cin >> b;
if (b != "-"){
r[i] = stoi(b);
st[r[i]] = true;
}
}
// 找到根节点
int root;
for (int i = 0; i < n; i++) {
if (!st[i]){
root = i;
break;
}
}
// 翻转二叉树
reverse(root);
// 层序遍历
bfs(root);
// 中序遍历
cout << endl;
cnt = 0;
dfs(root);
cout << in[0];
for (int i = 1; i < n; i++) {
cout << ' ' << in[i];
}
return 0;
}
前序和后序遍历序列
假设一个二叉树上所有结点的权值都互不相同。
我们可以通过后序遍历和中序遍历来确定唯一二叉树。
也可以通过前序遍历和中序遍历来确定唯一二叉树。
但是,如果只通过前序遍历和后序遍历,则有可能无法确定唯一二叉树。
现在,给定一组前序遍历和后序遍历,请你输出对应二叉树的中序遍历。
如果树不是唯一的,则输出任意一种可能树的中序遍历即可。
输入格式
第一行包含整数 N,表示结点数量。
第二行给出前序遍历序列。
第三行给出后序遍历序列。
一行中的数字都用空格隔开。
输出格式
首先第一行,如果树唯一,则输出 Yes,如果不唯一,则输出 No。
然后在第二行,输出树的中序遍历。
注意,如果树不唯一,则输出任意一种可能的情况均可。
数据范围
1≤N≤30
输入样例1:
7
1 2 3 4 6 7 5
2 6 7 4 5 3 1
输出样例1:
Yes
2 1 6 4 7 3 5
输入样例2:
4
1 2 3 4
2 4 3 1
输出样例2:
No
2 1 3 4
#include <iostream>
#include <string>
using namespace std;
const int N = 40;
int pre[N], post[N];
int cnt, n;
int dfs (int l1, int r1, int l2, int r2, string& in) {
// 已经构建完成,说明方案合法
if (l1 > r1)
return 1;
// 方案不合法
if (pre[l1] != post[r2])
return 0;
// 枚举左子树包含的节点数量
int cnt = 0;
// 暴力枚举有多少种情况
for (int i = l1; i <= r1; i++) {
string lin, rin;
int lcnt = dfs(l1 + 1, i, l2, l2 + i - l1 - 1, lin);
int rcnt = dfs(i + 1, r1, l2 + i - l1 - 1 + 1, r2 - 1, rin);
// 左右子树都存在,能够构建
if (lcnt > 0 && rcnt > 0) {
in = lin + to_string(pre[l1]) + ' ' + rin;
cnt += lcnt * rcnt;
if (cnt > 1)
break;
}
}
return cnt;
}
int main() {
cin >> n;
for (int i = 0; i < n; i++)
cin >> pre[i];
for (int i = 0; i < n; i++)
cin >> post[i];
string in;
// 求有多少种方案
cnt = dfs(0, n - 1, 0, n - 1, in);
if (cnt > 1)
cout << "No" << endl;
else
cout << "Yes" << endl;
in.pop_back();
cout << in << endl;
return 0;
}
后序遍历
假设二叉树上各结点的权值互不相同且都为正整数。
给定二叉树的前序遍历和中序遍历,请你输出二叉树的后序遍历的第一个数字。
输入格式
第一行包含整数 N,表示二叉树结点总数。
第二行给出二叉树的前序遍历序列。
第三行给出二叉树的中序遍历序列。
输出格式
输出二叉树的后序遍历的第一个数字。
数据范围
1≤N≤50000
输入样例:
7
1 2 3 4 5 6 7
2 3 1 5 4 7 6
输出样例:
3
#include <iostream>
#include <algorithm>
#include <unordered_map>
using namespace std;
const int N = 50010;
int pre[N], in[N];
unordered_map<int, int> pos;
int post, n;
void build(int il, int ir, int pl, int pr) {
int root = pre[pl];
int k = pos[root];
if (il < k)
build(il, k - 1, pl + 1, pl + 1 + k - 1 - il);
if (ir > k)
build(k + 1, ir, pl + 1 + k - 1 -il + 1, pr);
if (post == 0)
post = root;
}
int main () {
cin >> n;
for (int i = 0; i < n; i++) {
cin >> pre[i];
}
for (int i = 0; i < n; i++) {
cin >> in[i];
pos[in[i]] = i;
}
build(0, n - 1, 0, n -1);
cout << post << endl;
return 0;
}
AVL平衡二叉树
AVL树的根
AVL树是一种自平衡二叉搜索树。
在AVL树中,任何节点的两个子树的高度最多相差 1 个。
如果某个时间,某节点的两个子树之间的高度差超过 1,则将通过树旋转进行重新平衡以恢复此属性。
图 1−4 说明了旋转规则。
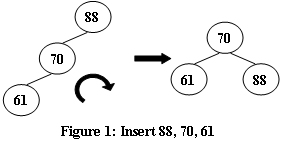
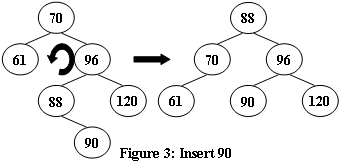
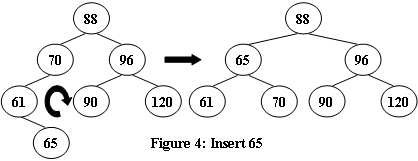
现在,给定插入序列,请你求出 AVL 树的根是多少。
输入格式
第一行包含整数 N,表示总插入值数量。
第二行包含 N 个不同的整数,表示每个插入值。
输出格式
输出得到的 AVL 树的根是多少。
数据范围
1≤N≤20
输入样例1:
5
88 70 61 96 120
输出样例1:
70
输入样例2:
7
88 70 61 96 120 90 65
输出样例2:
88
LL型 == > 右旋
- 将原来根(A)的左儿子变成新的根
- 现在根(B)的右儿子变成原来根(A)的左儿子(根据二叉搜索树定义确定)
- 现在根(B)的右儿子变成原来的根(A)

// 右旋操作
void R (int& u) {
// 原来根的左儿子变成新的根
int p = l[u];
// 现在根的右儿子变成原来根的左儿子
l[u] = r[p];
// 现在根的右儿子变成原来的根
r[p] = u;
update(u);
update(p);
u = p;
}
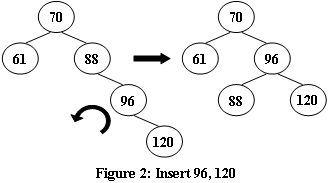
RR型 ==> 左旋
- 将原来根(A)的右儿子变成新的根
- 现在根(B)的左儿子变成原来根(A)的右儿子(根据二叉搜索树定义确定)
- 现在根(B)的左儿子变成原来的根(A)

// 左旋操作
void L (int& u) {
// 原来根的右儿子变成新的根
int p = r[u];
// 现在根的左儿子变成原来根的右儿子
r[u] = l[p];
// 现在根的左儿子变成原来的根
l[p] = u;
update(u);
update(p);
u = p;
}
LR型 == > 左旋 + 右旋

RL型 ==> 右旋 + 左旋

构建平衡二叉树
- 插入结点构建二叉搜索树
- 每次插入一个结点之后,获取根节点左右儿子高度差
- 左儿子结点的左右儿子高度差为1 == > LL 或者 RR(通过正负判断),否则就是 LR或者 RL
- 更新树的高度
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 30;
int l[N], r[N], v[N], h[N], idx;
// 更新树的高度
void update(int u) {
h[u] = max(h[l[u]], h[r[u]]) + 1;
}
// 右旋操作
void R (int& u) {
// 原来根的左儿子变成新的根
int p = l[u];
// 现在根的右儿子变成原来根的左儿子
l[u] = r[p];
// 现在根的右儿子变成原来的根
r[p] = u;
update(u);
update(p);
u = p;
}
// 左旋操作
void L (int& u) {
// 原来根的右儿子变成新的根
int p = r[u];
// 现在根的左儿子变成原来根的右儿子
r[u] = l[p];
// 现在根的左儿子变成原来的根
l[p] = u;
update(u);
update(p);
u = p;
}
// 获取左右儿子的高度差
int get_balance(int u) {
return h[l[u]] - h[r[u]];
}
void insert(int& u, int w) {
if (u == 0) {
u = ++idx;
v[u] = w;
}
// 插到根节点的左子树
else if (w < v[u]) {
insert(l[u], w);
if (get_balance(u) == 2) {
// LL型:右旋根节点
if (get_balance(l[u]) == 1)
R(u);
// LR型:左旋左子树,右旋根
else {
L(l[u]);
R(u);
}
}
}
// 插入到根节点的右子树
else {
insert(r[u], w);
if (get_balance(u) == -2) {
// RR型:左旋根节点
if (get_balance(r[u]) == -1)
L(u);
// LR型:右旋右子树,左旋根
else {
R(r[u]);
L(u);
}
}
}
// 更新树的高度
update(u);
}
int main() {
int n;
cin >> n;
int root = 0;
while (n--) {
int w;
cin >> w;
insert(root, w);
}
cout << v[root] << endl;
return 0;
}
判断完全AVL树
AVL树是一种自平衡二叉搜索树。
在AVL树中,任何节点的两个子树的高度最多相差 1 个。
如果某个时间,某节点的两个子树之间的高度差超过 1,则将通过树旋转进行重新平衡以恢复此属性。
图 1−4 说明了旋转规则。
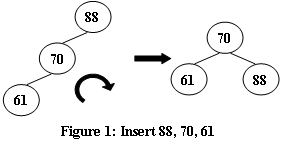
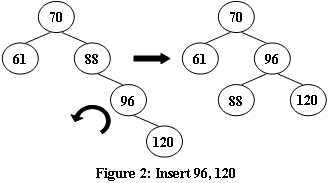
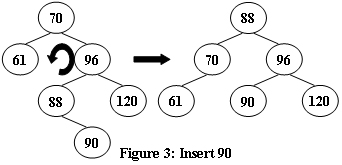
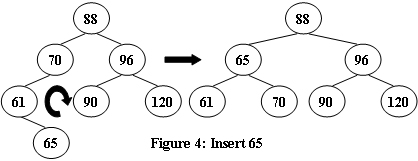
现在,给定插入序列,请你输出得到的AVL树的层序遍历,并判断它是否是完全二叉树。
输入格式
第一行包含整数 N,表示插入序列中元素个数。
第二行包含 N 个不同的整数表示插入序列。
输出格式
第一行输出得到的AVL树的层序遍历序列。
第二行,如果该AVL树是完全二叉树,则输出 YES,否则输出 NO。
数据范围
1≤N≤20
输入样例1:
5
88 70 61 63 65
输出样例1:
70 63 88 61 65
YES
输入样例2:
8
88 70 61 96 120 90 65 68
输出样例2:
88 65 96 61 70 90 120 68
NO
- 构建平衡二叉树
- BFS判断是否是完全二叉树:pos从1开始记录,左右儿子按2 * i 和2 * i + 1 记录,若记录大于结点数n,则不是完全二叉树
#include <iostream>
#include <queue>
using namespace std;
const int N = 30;
// 记录左右儿子
int l[N], r[N];
// 记录节点权值
int v[N];
// 记录每个节点高度
int h[N];
// 记录层序遍历结果
int level[N];
// 记录节点编号
int pos[N];
int idx, n, cnt;
// 更新节点的高度
void update(int u) {
h[u] = max(h[l[u]], h[r[u]]) + 1;
}
// 右旋
void R(int& u) {
// 原来根的左儿子变成新的根
int p = l[u];
// 现在根的右儿子变成原来根的左儿子
l[u] = r[p];
// 现在根的右儿子变成原来的根
r[p] = u;
update(u);
update(p);
u = p;
}
// 左旋
void L(int& u) {
// 原来根的右儿子变成新的根
int p = r[u];
// 现在根的左儿子变成原来根的右儿子
r[u] = l[p];
// 现在根的左儿子变成原来的根
l[p] = u;
update(u);
update(p);
u = p;
}
// 获取左右儿子高度差
int get_balance(int u) {
return h[l[u]] - h[r[u]];
}
// 插入新节点到u的左儿子或右儿子
void insert(int& u, int w) {
if (u == 0) {
u = ++idx;
v[u] = w;
}
// 插到根节点的左子树
else if (w < v[u]) {
insert(l[u], w);
if (get_balance(u) == 2) {
// LL型:右旋根节点
if (get_balance(l[u]) == 1)
R(u);
// LR型:左旋左子树,右旋根
else {
L(l[u]);
R(u);
}
}
}
// 插入到根节点的右子树
else {
insert(r[u], w);
if (get_balance(u) == -2) {
// RR型:左旋根节点
if (get_balance(r[u]) == -1)
L(u);
// LR型:右旋右子树,左旋根
else {
R(r[u]);
L(u);
}
}
}
// 更新树的高度
update(u);
}
bool bfs(int u) {
queue<int> q;
q.push(u);
pos[u] = 1;
bool res = true;
while (!q.empty()) {
int t = q.front();
q.pop();
level[cnt++] = t;
if (pos[t] > n)
res = false;
if (l[t]) {
q.push(l[t]);
pos[l[t]] = pos[t] * 2;
}
if (r[t]) {
q.push(r[t]);
pos[r[t]] = pos[t] * 2 + 1;
}
}
return res;
}
int main() {
int root = 0;
cin >> n;
for (int i = 0; i < n; i++) {
int w;
cin >> w;
insert(root, w);
}
bool res = bfs(root);
cout << v[level[0]];
for (int i = 1; i < n; i++) {
cout << ' ' << v[level[i]];
}
cout << endl;
if (res)
cout << "YES" << endl;
else
cout << "NO" << endl;
return 0;
}
判断红黑树
数据结构中有一类平衡的二叉搜索树,称为红黑树。
它具有以下 5 个属性:
- 节点是红色或黑色。
- 根节点是黑色。
- 所有叶子都是黑色。(叶子是 NULL节点)
- 每个红色节点的两个子节点都是黑色。
- 从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点。
例如,下列三张图中,左图中的二叉树是红黑树,其余两图中的二叉树不是红黑树。
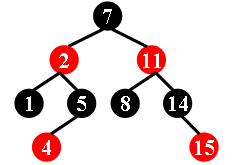
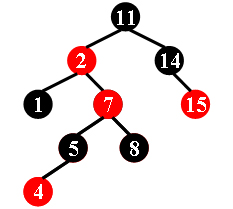
现在,对于每个给定的二叉搜索树,请你判断它是否是合法的红黑树。
注意
给定的前序遍历序列可能不合法,即无法构建出合法二叉搜索树。
输入格式
第一行包含整数 K,表示共有 K 组测试数据。
每组测试数据,第一行包含整数 N,表示二叉搜索树的节点数量。
第二行给出了这个二叉搜索树的前序遍历。
注意,虽然所有节点的权值都为正,但是我们使用负号表示红色节点。
各节点权值互不相同。
输入样例与题目中三个图例相对应。
输出格式
对于每组数据,如果是合法红黑树则输出一行 Yes,否则输出一行 No。
数据范围
1≤K≤30,
1≤N≤30
输入样例:
3
9
7 -2 1 5 -4 -11 8 14 -15
9
11 -2 1 -7 5 -4 8 14 -15
8
10 -7 5 -6 8 15 -11 17
输出样例:
Yes
No
No
- 通过前序和中序序列构建树(注意判断前序序列是否合法)
- 判断左右子树中黑色结点个数是否相同
- 红色结点下面必须是两个黑色结点判断
- 统计黑色结点数
#include <iostream>
#include <unordered_map>
#include <algorithm>
using namespace std;
const int N = 40;
int pre[N], in[N];
unordered_map<int, int> pos;
bool ans;
int build (int il, int ir, int pl, int pr, int& sum) {
int root = pre[pl];
int k = pos[abs(root)];
// 如果前序序列不合法,返回false
if (k < il || k > ir) {
ans = false;
return 0;
}
int left = 0;
int right = 0;
int ls = 0;
int rs = 0;
// 构建树的过程
if (il < k)
left = build(il, k - 1, pl + 1, pl + 1 + k - 1 - il, ls);
if (k < ir)
right = build(k + 1, ir, pl + 1 + k - 1 - il + 1, pr, rs);
// 左右子树中黑色点的个数不同
if (ls != rs)
ans = false;
sum = ls;
// 每个红色节点下面必须是两个黑色节点
if (root < 0) {
if (left < 0 || right < 0)
ans = false;
}
// 是黑色节点,则++
else
sum++;
return root;
}
int main() {
int T;
cin >> T;
while (T--) {
int n;
cin >> n;
for (int i = 0; i < n; i++) {
cin >> pre[i];
// 存在正负:存中序节点我们使用绝对值
in[i] = abs(pre[i]);
}
sort(in, in + n);
pos.clear();
for (int i = 0; i < n; i++)
pos[in[i]] = i;
ans = true;
int sum;
int root = build(0, n - 1, 0, n - 1, sum);
if (root < 0)
ans = false;
if (ans)
cout << "Yes" << endl;
else
cout << "No" << endl;
}
}
公共祖先
最低公共祖先
树中两个结点 U 和 V 的最低公共祖先(LCA)是指同时具有 U 和 V 作为后代的最深结点。
二叉搜索树 (BST) 递归定义为具有以下属性的二叉树:
- 若它的左子树不空,则左子树上所有结点的值均小于它的根结点的值
- 若它的右子树不空,则右子树上所有结点的值均大于或等于它的根结点的值
- 它的左、右子树也分别为二叉搜索树
现在给定 BST 中的任意两个结点,请你找出它们的最低公共祖先。
输入格式
第一行包含两个整数 M 和 N,分别表示询问结点对数以及二叉搜索树中的结点数量。
第二行包含 N 个不同整数,表示该二叉搜索树的前序遍历序列。
接下来 M 行,每行包含两个不同的整数 U 和 V,表示一组询问。
所有结点权值均在 int 范围内。
输出格式
对于每对给定的 U 和 V,输出一行结果。
如果 U 和 V 的 LCA 是 A,且 A 不是 U 或 V,则输出 LCA of U and V is A.。
如果 U 和 V 的 LCA 是 A,且 A 是 U 或 V 中的一个,则输出 X is an ancestor of Y.,其中 X 表示 A,Y 表示另一个结点。
如果 U 或 V 没有在 BST 中找到,则输出 ERROR: U is not found. 或 ERROR: V is not found. 或 ERROR: U and V are not found.。
数据范围
1≤M≤1000,
1≤N≤10000
输入样例:
6 8
6 3 1 2 5 4 8 7
2 5
8 7
1 9
12 -3
0 8
99 99
输出样例:
LCA of 2 and 5 is 3.
8 is an ancestor of 7.
ERROR: 9 is not found.
ERROR: 12 and -3 are not found.
ERROR: 0 is not found.
ERROR: 99 and 99 are not found.
- 存储只需要存储结点的父节点,构建树的时候找所有点深度
- 将比较低的点向上移动,找到与另一个点同一深度
- 两个点同步向上找到相同的点
题中结点权值是int范围,我们可以使用hash表做一个映射,映射到0 ~ N - 1,减少时间复杂度前面的常数
#include <iostream>
#include <unordered_map>
#include <algorithm>
using namespace std;
const int N = 10010;
int m, n;
int in[N], pre[N];
// 存储离散化处理之前的数据
int seq[N];
// 映射:离散化处理
unordered_map<int, int> pos;
// 记录每个节点的父节点
int p[N];
int depth[N];
// 构建二叉树,并记录每个节点的层数
int build (int il, int ir, int pl, int pr, int d) {
int root = pre[pl];
// 进行了映射处理,根节点的值就是相应根节点在中序序列的下标
int k = root;
depth[root] = d;
// 记录左右儿子的父节点为root
if (il < k)
p[build(il, k - 1, pl + 1, pl + 1 + k - 1- il, d + 1)] = root;
if (k < ir)
p[build(k + 1, ir, pl + 1 + k - 1 - il + 1, pr, d + 1)] = root;
return root;
}
int main() {
cin >> m >> n;
for (int i = 0; i < n; i++) {
cin >> pre[i];
seq[i] = pre[i];
}
sort(seq, seq + n);
// 把int范围内的数映射到 0 ~ n -1,减少常数级别的操作,pos中的key存的就是原来的值
for (int i = 0; i < n; i++) {
pos[seq[i]] = i;
in[i] = i;
}
for (int i = 0; i < n; i++)
pre[i] = pos[pre[i]];
build(0, n - 1, 0, n - 1, 0);
while (m--) {
int a, b;
cin >> a >> b;
// 查询合法
if (pos.count(b) && pos.count(a)) {
a = pos[a];
b = pos[b];
// 记录下来查询的值
int x = a;
int y = b;
// 找公共祖先节点
while (a != b) {
// b的深度更深,往上找父节点
if (depth[a] < depth[b])
b = p[b];
else
a = p[a];
}
if (a != x && b != y)
printf("LCA of %d and %d is %d.\n", seq[x], seq[y], seq[a]);
else if (a == x)
printf("%d is an ancestor of %d.\n", seq[x], seq[y]);
else
printf("%d is an ancestor of %d.\n", seq[y], seq[x]);
}
else if (pos.count(a) == 0 && pos.count(b) == 0)
printf("ERROR: %d and %d are not found.\n", a, b);
else if (pos.count(a) == 0)
printf("ERROR: %d is not found.\n", a);
else
printf("ERROR: %d is not found.\n", b);
}
return 0;
}
二叉树中最低公共祖先
树中两个结点 U 和 V 的最低公共祖先(LCA)是指同时具有 U 和 V 作为后代的最深结点。
给定二叉树中的任何两个结点,请你找到它们的 LCA。
输入格式
第一行包含两个整数 M 和 N,分别表示询问结点对数以及二叉树中的结点数量。
接下来两行,每行包含 N 个不同的整数,分别表示二叉树的中序和前序遍历。
保证二叉树可由给定遍历序列唯一确定。
接下来 M 行,每行包含两个不同的整数 U 和 V,表示一组询问。
所有结点权值均在 int 范围内。
输出格式
对于每对给定的 U 和 V,输出一行结果。
如果 U 和 V 的 LCA 是 A,且 A 不是 U 或 V,则输出 LCA of U and V is A.。
如果 U 和 V 的 LCA 是 A,且 A 是 U 或 V 中的一个,则输出 X is an ancestor of Y.,其中 X 表示 A,Y 表示另一个结点。
如果 U 或 V 没有在二叉树中找到,则输出 ERROR: U is not found. 或 ERROR: V is not found. 或 ERROR: U and V are not found.。
数据范围
1≤M≤1000,
1≤N≤10000
输入样例:
6 8
7 2 3 4 6 5 1 8
5 3 7 2 6 4 8 1
2 6
8 1
7 9
12 -3
0 8
99 99
输出样例:
LCA of 2 and 6 is 3.
8 is an ancestor of 1.
ERROR: 9 is not found.
ERROR: 12 and -3 are not found.
ERROR: 0 is not found.
ERROR: 99 and 99 are not found.
#include <iostream>
#include <unordered_map>
using namespace std;
const int N = 10010;
int n, m;
int pre[N], in[N], seq[N];
unordered_map<int, int> pos;
int p[N];
int depth[N];
int build (int il, int ir, int pl, int pr, int d) {
int root = pre[pl];
int k = root;
depth[root] = d;
if (il < k)
p[build(il, k - 1, pl + 1, pl + 1 + k - 1 - il, d + 1)] = root;
if (k < ir)
p[build(k + 1, ir, pl + 1 + k - 1 - il + 1, pr, d + 1)] = root;
return root;
}
int main() {
cin >> m >> n;
// 读入中序序列并映射
for (int i = 0; i < n; i++) {
cin >> seq[i];
pos[seq[i]] = i;
in[i] = i;
}
// 读入前序序列并做好映射
for (int i = 0; i < n; i++) {
cin >> pre[i];
pre[i] = pos[pre[i]];
}
build(0, n - 1, 0, n - 1, 0);
while (m--) {
int a, b;
cin >> a >> b;
// 查询合法
if (pos.count(b) && pos.count(a)) {
a = pos[a];
b = pos[b];
// 记录下来查询的值
int x = a;
int y = b;
// 找公共祖先节点
while (a != b) {
// b的深度更深,往上找父节点
if (depth[a] < depth[b])
b = p[b];
else
a = p[a];
}
if (a != x && b != y)
printf("LCA of %d and %d is %d.\n", seq[x], seq[y], seq[a]);
else if (a == x)
printf("%d is an ancestor of %d.\n", seq[x], seq[y]);
else
printf("%d is an ancestor of %d.\n", seq[y], seq[x]);
}
else if (pos.count(a) == 0 && pos.count(b) == 0)
printf("ERROR: %d and %d are not found.\n", a, b);
else if (pos.count(a) == 0)
printf("ERROR: %d is not found.\n", a);
else
printf("ERROR: %d is not found.\n", b);
}
return 0;
}