区间合并问题

区间合并是一类比较经典的问题：将一部分有交集的区间进行合并，这里就区间合并算法做一个简单的分析

给定 n 个区间 [li,ri]，要求合并所有有交集的区间。注意如果在端点处相交，也算有交集。输出合并完成后的区间个数。例如：[1,3]和[2,6]可以合并为一个区间[1,6]。

输入格式

第一行包含整数n。接下来n行，每行包含两个整数 l 和 r。

输出格式

共一行，包含一个整数，表示合并区间完成后的区间个数。

数据范围

$1≤n≤100000, −10^9≤li≤ri≤10^9$

输入样例：

5
1 2
2 4
5 6
7 8
7 9

输出样例：

3

• 按区间左端点排序
• 分情况合并

经过左端点排序之后，只会出现下面的情况：

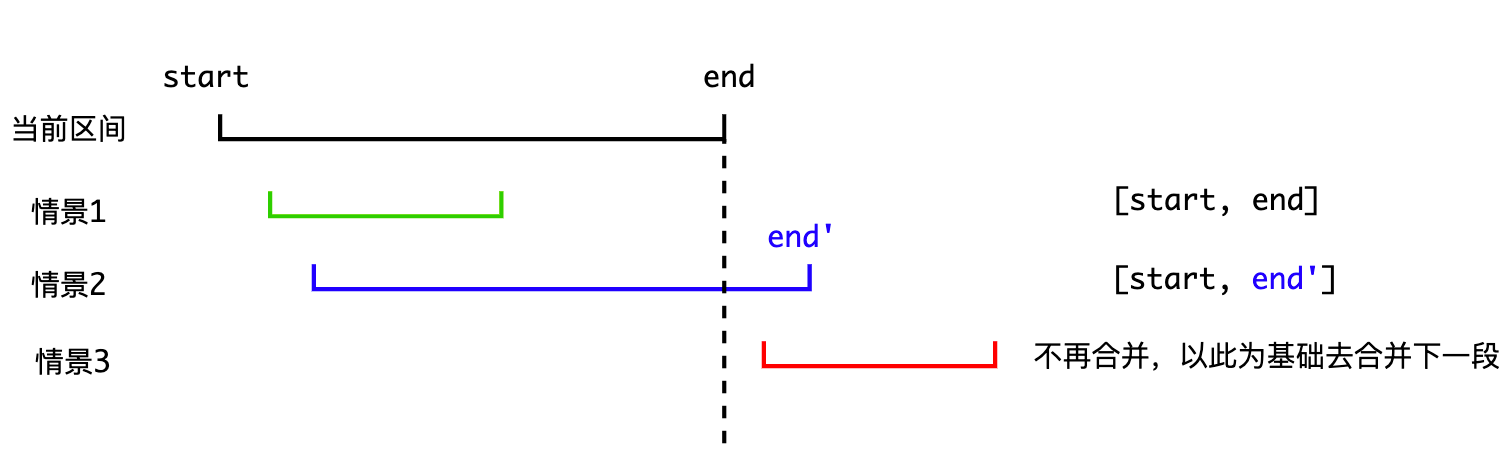
• 情况一：当前区间完全被上一区间覆盖，直接跳过
• 情况二：将当前区间的右端点更新为上一区间的右端点，达到区间延长的效果
• 情况三：当前区间的左端点严格大于上一区间的右端点，则表示该区间不能合并，更新区间去合并下一段

#include <iostream>
#include <algorithm>
#include <vector>

using namespace std;

typedef pair<int, int> PII;

vector<PII> seg;
int n;

int merge(vector<PII>& seg) {
    vector<PII> res;
    // sort默认先排first位置
    sort(seg.begin(), seg.end());
    int start = -2e9, end = -2e9;
    for (auto item : seg) {
        // 没有交集
        if (item.first > end) {
            // 如果是第一段就先不加入到结果集
            if (start != -2e9) 
                res.push_back({start, end});
            start = item.first;
            end = item.second;
        }
        // 合并操作
        else 
            end = max(end, item.second);
    }
    // 最后一段还没有加入到结果集中，这里判断防止空的情况
    if (start != -2e9)
        res.push_back({start, end});
    return res.size();
}

int main() {
   cin >> n;
   for (int i = 0; i < n; i++) {
       int l, r;
       cin >> l >> r;
       seg.push_back({l, r});
   }
   cout << merge(seg) << endl;
   return 0;
}