浅谈Trie树

什么是Trie树？

Trie树又称单词查找树，是一种树形结构。典型应用是用于统计、排序、保存和查找大量的字符串（但不仅限于字符串），所以经常被搜索引擎系统用于文本词频统计。

根节点不包含字符，除根节点外每一个节点都只包含一个字符； 从根节点到某一节点，路径上经过的字符连接起来，为该节点对应的字符串； 每个节点的所有子节点包含的字符都不相同。

它的优点是：利用字符串的公共前缀来减少查询时间，最大限度地减少无谓的字符串比较

例如存储字符串集合：${b， abc， abd， abcd， abcd， bcd， efg， hij}$

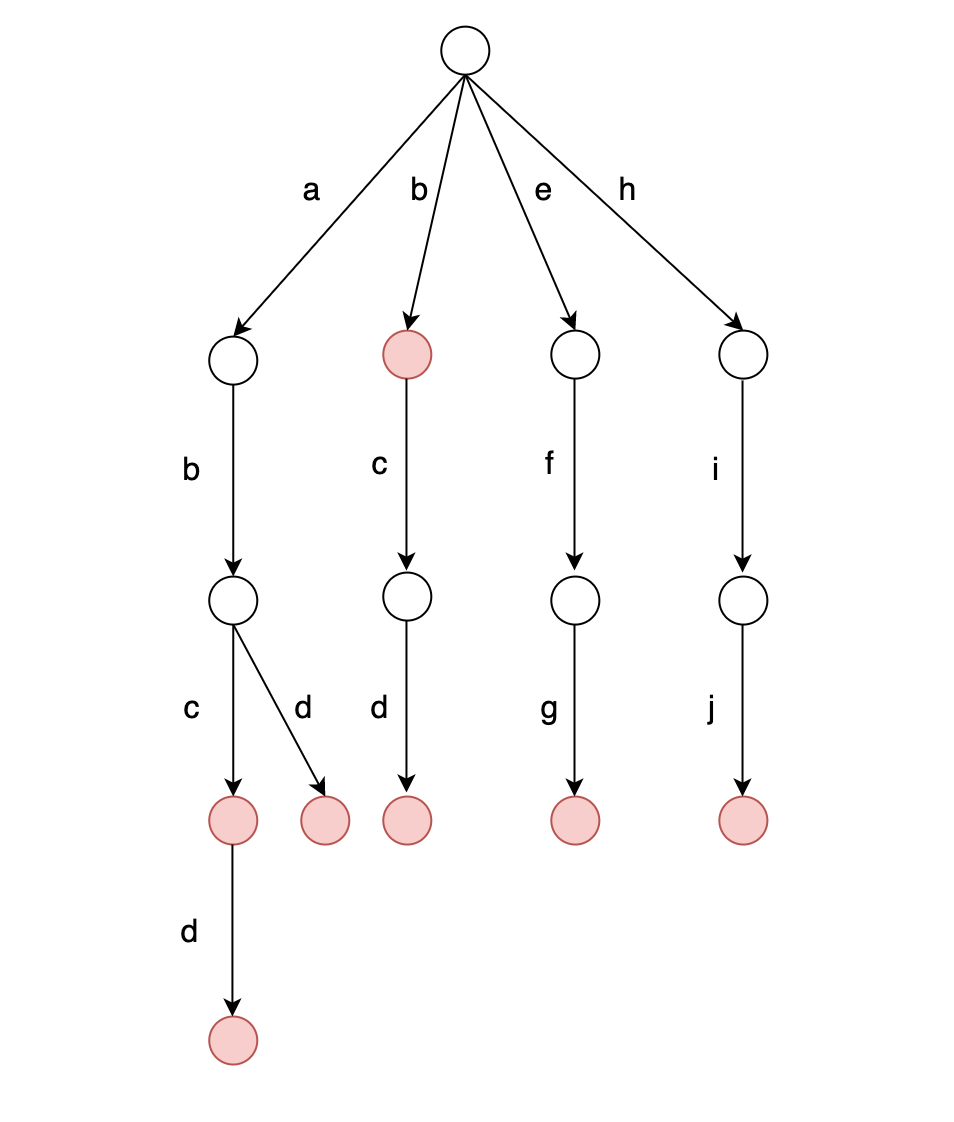
Trie树基本操作

这里以字符串为例

理解核心数据结构

• $idx$ ：用不同的$idx$值来记录结点，以下标来记录每一个字符的位置，每次插入一个字符，$idx++$

• $son[N] [26]$ ：表示当前结点的儿子，其中存放的是子节点对应的$idx$；其中第一维是父节点对应的$idx$，这里的$N$代表字符串的总长度，所以$idx$永远在这个范围之内。第二维的计数是子节点$('a' - '0')$的值为二维下标，对于字母而言最多有$26$个子结点。比如：$son[1] [0]=2$表示$1$结点的一个值为$a$的子结点为结点$2$；如果$son[1] [0]= 0$，则意味着没有值为$a$子结点

• $cnt[N]$ ：$cnt[p]$标记以$p$结尾的字符串的个数。以$“abc”$字符串为例，最后一个字符$‘c’$对应的$idx$作为$cnt$数组的下标。数组的值是该$idx$对应的个数

插入

• 遍历字符串的每一个字符
  • 将字符映射到$0 - 25$
  • 子节点没有该字符，则添加进来
• 遍历结束，将字符串最后一个位置对应的$trie$树结点$idx$对应的$cnt$数组计数++

#include <iostream>
using namespace std;

// N受字符串总长度的限制
const int N = 100010;

int son[N][26];
int idx;
int cnt[N];
char str[N];

/**
 * @brief 将字符串添加到Trie树中
 * @param str 
 */
void insert (char* str) {
    int p = 0;
    for (int i = 0; str[i]; i++) {
        // 将字符映射到0-25
        int u = str[i] - 'a';
        // 没有该字符，添加进来
        if (!son[p][u])
            son[p][u] = ++idx;
        p = son[p][u];
    }
    // 此时的p就是str中最后一个字符对应的trie树的位置idx
    cnt[p]++;
}

查找

• 遍历字符串的每一个字符，如果其中任一个字符没有在$Trie$树中找到相应结点则返回$0$
• 遍历结束，返回该字符串最后一个字符对应$idx$的$cnt$数组的值

/**
 * @brief 查找字符串str出现的次数
 * @param str 
 * @return int 
 */
int query (char* str) {
    int p = 0;
    for (int i = 0; str[i]; i++) {
        int u = str[i] - 'a';
        if (!son[p][u])
            return 0;
        p = son[p][u];
    }
    return cnt[p];
}

最大异或对

在给定的$N$个整数$A_{1}，A_{2}……A_{N}$中选出两个进行$xor$（异或）运算，得到的结果最大是多少？

输入格式

第一行输入一个整数$N$

第二行输入$N$个整数$A_{1}～A_{N}$

输出格式

输出一个整数表示答案。

数据范围

$1≤ N ≤10^5, 0≤ A_{i}<2^{31}$

输入样例：

3
1 2 3

输出样例：

3

暴力枚举

算法时间复杂度$O(n^2)$

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 100010;

int a[N];
int n;

int main() {
    cin >> n;
    for (int i  = 0; i < n; i++) 
        cin >> a[i];
    
    int res = 0;
    for (int i = 0; i < n; i++) 
        for (int j = 0; j < n; j++)
            res = max(res, a[i] ^ a[j]);
   	
    cout << res << endl;
}

使用Trie树优化

• 优化目标：当我们去枚举每一个$A_{i}$的时候，我们相当于要从$A_{1} - A_{n}$之间选出一个$A_{j}$使得异或值最大，那么就相当于在我们选的时候，用Trie树进行优化

• 对于每一个$A_{i}$我们都可以写成$32$位$2$进制的形式 $\underbrace{11010101010...0101110}_{32}$，然后将每个数加进Trie树里面， 我们要做的就是从最高位开始尽可能找到不同的那个结点往下走，每走一步，就会减去一半的规模，所以最后的时间复杂度为$O(n log_{2} n)$

#include <iostream>

using namespace std;

const int N = 100010, M = 3100010;

int son[M][2], idx;
int n;
int a[N];

void insert(int x) {
    int p = 0;
    for (int i = 30; i >= 0; i--) {
        // x >> i & 1：从高位开始取
        int u = son[p][x >> i & 1];
        if (!u)
            son[p][x >> i & 1] = ++idx;
        p = son[p][x >> i & 1];
    }
}

int query(int x) {
    int p = 0, res = 0; 
    for (int i = 30; i >= 0; i--) {
        // 从高位开始尽量寻找不同，这样异或出来是最大的
        int u = x >> i & 1;
        if (son[p][!u]) {
            res += 1 << i;
            p = son[p][!u];
        }
        else
            p = son[p][u];
    }
    return res;
}

int main() {
    cin >> n;
    for (int i = 0; i < n; i++) {
        cin >> a[i];
        insert(a[i]);
    }
    
    int res = 0;
    for (int i = 0; i < n; i++) 
        res = max(res, query(a[i]));
    cout << res << endl;
    return 0;
}