二分查找是解决很多查找类题目的常用方法,它可以达到O(log n)的时间复杂度。对于浮点数的二分比较简单,但涉及到整数的二分,边界情况的考虑就显得非常重要,思路很简单,细节是魔鬼。这里总结了两套模板对解题有很大的帮助
一般而言,当一个题目出现以下特征,就应该联想到要使用二分查找
- 待查找的数组有序或者部分有序
- 要求时间复杂度低于O(n)
整数二分
两个模板
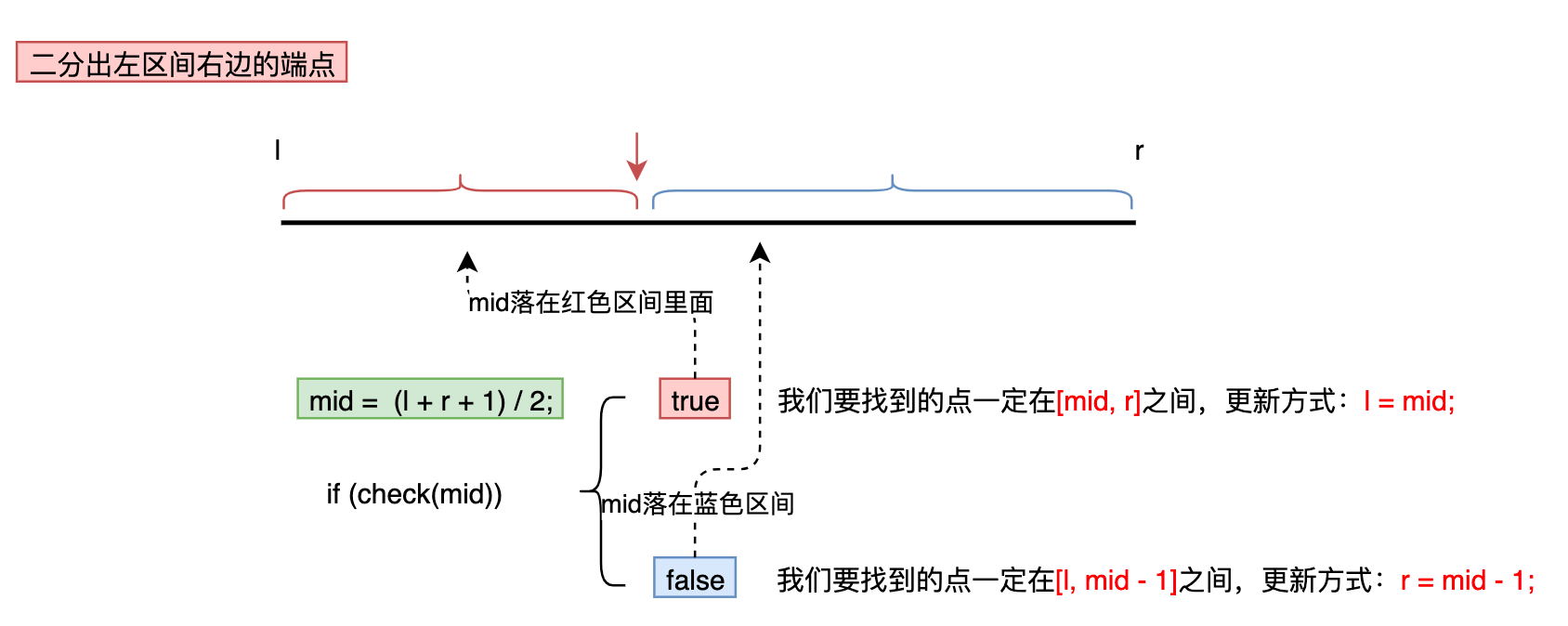
- 区间被划分为和时可用
- 这里在加的原因是:当时,由于C++向下取整:导致死循环,所以要加
int binarySearch_1 (int l, int r) {
int l = 0, r = n - 1;
while (l < r) {
mid = l + r + 1 >> 1;
if (check(mid)) // check()判断mid是否满足性质的函数:具体根据题目描述来写
l = mid;
else
r = mid - 1;
}
return l;
}
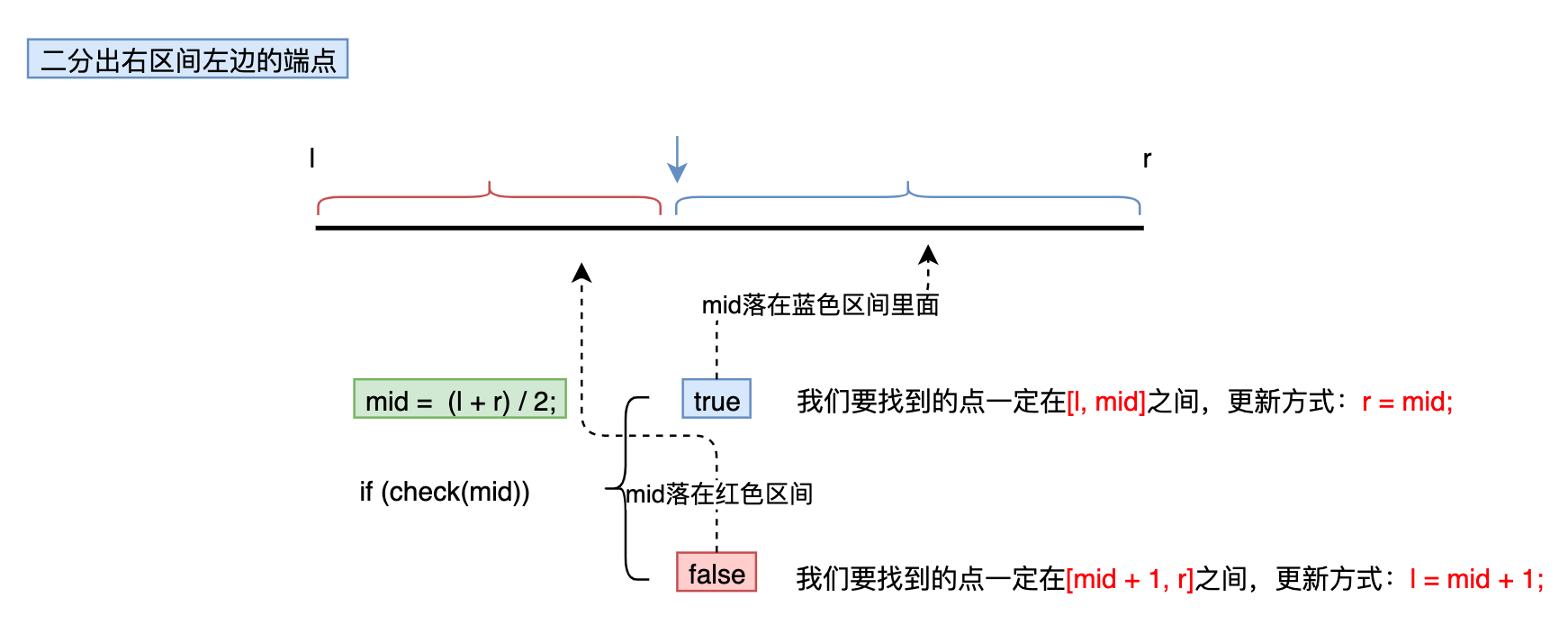
- 区间被划分为和时可用
int binarySearch_2 (int l, int r) {
int l = 0, r = n - 1;
while (l < r) {
mid = l + r >> 1;
if (check(mid)) // check()判断mid是否满足性质的函数:具体根据题目描述来写
r = mid;
else
l = mid + 1;
}
return l;
}
模板使用技巧
在做题的过程中
- 我们只需要先写
- 根据具体题目写好函数,找到更新方式,确定到底是还是
- 若是的情况,我们只需要在第一个步骤里面把二分时的取值进行加
- 的情况,另一边就是; 的情况,另一边就是
例题
给定一个按照升序排列的长度为n的整数数组,以及 q 个查询。对于每个查询,返回一个元素k的起始位置和终止位置(位置从0开始计数)。如果数组中不存在该元素,则返回“-1 -1”。
输入格式
第一行包含整数n和q,表示数组长度和询问个数。第二行包含n个整数(均在1~10000范围内),表示完整数组。接下来q行,每行包含一个整数k,表示一个询问元素。
输出格式
共q行,每行包含两个整数,表示所求元素的起始位置和终止位置。如果数组中不存在该元素,则返回“-1 -1”。
数据范围
输入样例:
6 3
1 2 2 3 3 4
3
4
5
输出样例:
3 4
5 5
-1 -1
#include<iostream>
using namespace std;
const int N = 100010;
int q[N];
int main() {
int n, m;
cin >> n >> m;
for (int i = 0; i < n; i++)
cin >> q[i];
while (m--) {
int x;
cin >> x;
int l = 0, r = n - 1;
while (l < r) {
int mid = l + r >> 1;
// 找左端点:q[mid] >= x确定要找的左端点一定在[l, mid]之间,更新r = mid
if (q[mid] >= x)
r = mid;
// r = mid,对应l就是mid + 1,对应第二个模板,前面mid不需要修改
else
l = mid + 1;
}
if (q[l] != x)
cout << "-1 -1" << endl;
else {
cout << l << ' ';
l = 0, r = n - 1;
while (l < r) {
int mid = l + r + 1 >> 1;
// 找右端点:q[mid] <= x确定要找的右端点一定在[mid, r]之间,更新l = mid
if (q[mid] <= x)
l = mid;
// l = mid,对应r就是mid - 1,对应第一个模板,前面mid修改+1
else
r = mid - 1;
}
cout << l << endl;
}
}
return 0;
}
浮点数二分
给定一个浮点数,求它的三次方根。
对于这一类浮点数二分的题目:当足够小时,我们就假定已经找完,用公式表示为 ,此时有个精度问题如果要求保留六位小数则,总要比保留的位数多两位。
输入格式
共一行,包含一个浮点数。
输出格式
共一行,包含一个浮点数,表示问题的解。注意,结果保留6位小数。
数据范围
输入样例:
1000.00
输出样例:
10.000000
#include <iostream>
using namespace std;
int main() {
double x;
cin >> x;
double l = -10000, r = 10000;
// 通常比要求精度提高2位
while (r - l > 1e-8) {
double mid = (l + r) / 2;
// 浮点数二分不用考虑边界问题
if (mid * mid * mid >= x)
r = mid;
else
l = mid;
}
printf("%lf\n", l);
return 0;
}
