掐死KMP算法

KMP算法是一个效率非常高的字符串匹配算法。不过其难以理解。在这里总结一下最容易理解的KMP算法。

KMP算法完成的任务是：给定两个字符串A和B，长度分别为n和m，判断B是否在A中出现，如果出现则返回出现的位置。

BF算法

在介绍$KMP$算法之前，我们首先看一下暴力匹配算法。暴力匹配非常容易理解：那就是暴力去遍历字符串$A$的每一个位置，然后从该位置开始和$B$进行匹配，但是这种方法的复杂度是$O(nm)$

int BF(string A, string B) {
    int n = A.size();
    int m = B.size();
    for (int i = 0; i < n - m; i++) {
        int j = 0;
        while (j < m; j++) {
            if (A[i] != B[j])
                break;
        }
        // 全部匹配，输出下标
        if (j == m)
			cout << i << endl;
    }
    // 没有找到
    return -1;
}

KMP算法

KMP原理

对于暴力算法，如果出现不匹配字符，同时回退$A$和$B$的指针。最主要的问题在于：如果字符串中重复的字符比较多，该算法就显得很蠢。$KMP$算法通过一个$O(m)$的预处理，使匹配的复杂度降为$O(n+m)$

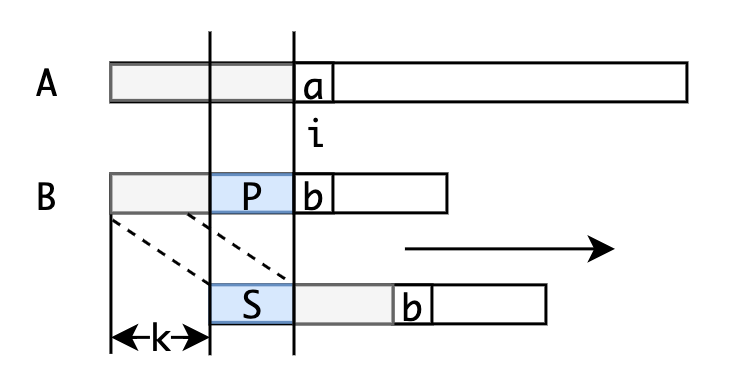
在字符串$A$中寻找$B$，当匹配到位置$i$时两个字符串不相等，这时我们需要将字符串$B$向前移动。常规方法是每次向前移动一位，但是它没有考虑前$i-1$位已经比较过这个事实，所以效率不高。事实上，如果我们提前计算某些信息，就有可能一次前移多位。假设我们根据已经获得的信息知道可以前移$k$位，我们分析移位前后的$B$有什么特点。我们可以得到如下的结论：

• S段字符串是$B$的一个前缀
• $P$段字符串是$B$的一个后缀
• $P$段和$S$段字符串长度为 $i - k - 1$
• $P$段字符串和$S$段字符串相等

所以前移$k$位之后，可以继续比较位置$i$的前提是$B$的前$i-1$个位置满足：长度为$i-k-1$的前缀S和后缀P相同。只有这样，我们才可以前移$k$位后从新的位置继续比较

$KMP$算法的核心即是计算字符串$B$每一个位置之前的字符串的前缀和后缀公共部分的最大长度。获得$B$每一个位置的最大公共长度之后，就可以利用该最大公共长度快速和字符串$A$比较。

当每次比较到两个字符串的字符不同时，我们就可以根据最大公共长度将字符串$B$向前移动(k = 已匹配长度 - 最大公共长度)位，接着继续比较下一个位置。事实上，字符串$B$的前移只是概念上的前移，只要我们在比较的时候从最大公共长度之后比较$B$和$A$即可达到字符串$B$前移的目的，在整个匹配过程中都不会出现字符串$A$的指针走回头路的情况

核心next数组

$KMP$算法的难点在于，如何计算$next$数组（仅仅与要去匹配的字符串$B$有关）中的信息？如何根据这些信息正确地移动字符串$B$的指针？

在这里我们需要注意的是

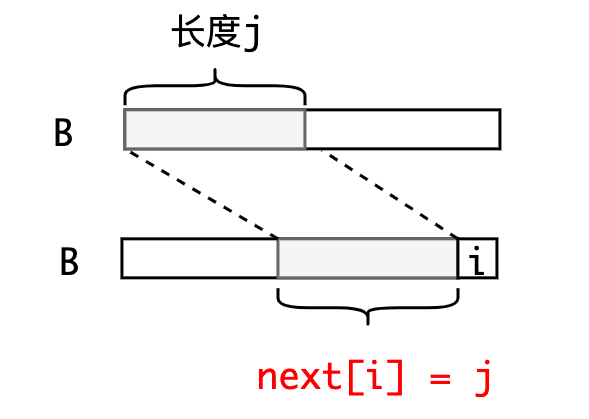
• $next$数组表示的是长度信息，并且下标从$1$开始
• $next[i] = j$表达的含义是：长度为$i$的字符串的前缀和后缀最大公共长度为$j$。表现在字符串$B$中就是：$B$中$[0, j - 1]$长度为$j$这一段和$[i - j, i - 1]$长度为$j$这一段是匹配相等的，并且是最大的匹配段

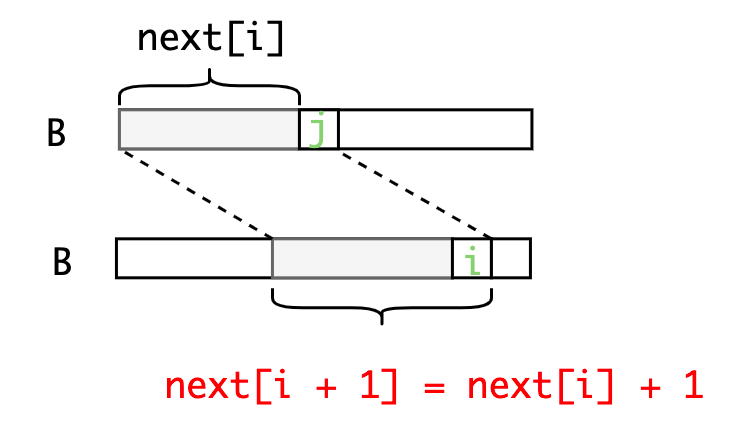
那么现在我们已知$next[i]$，要求$next[i + 1]$，我们怎么做？

• 如果位置$i$和$next[i] (j)$处两个字符相同，$B[i] = B[j]$那么$next[i + 1] = next[i] + 1$

• 如果这两个位置的字符不相同：我们可以将长度为$next[i]$的字符串继续分割，获得其最大公共长度$next[next[i]]$，然后再和位置$i$的字符比较。这是因为长度为$next[i]$前缀和后缀都可以分割成上部的构造

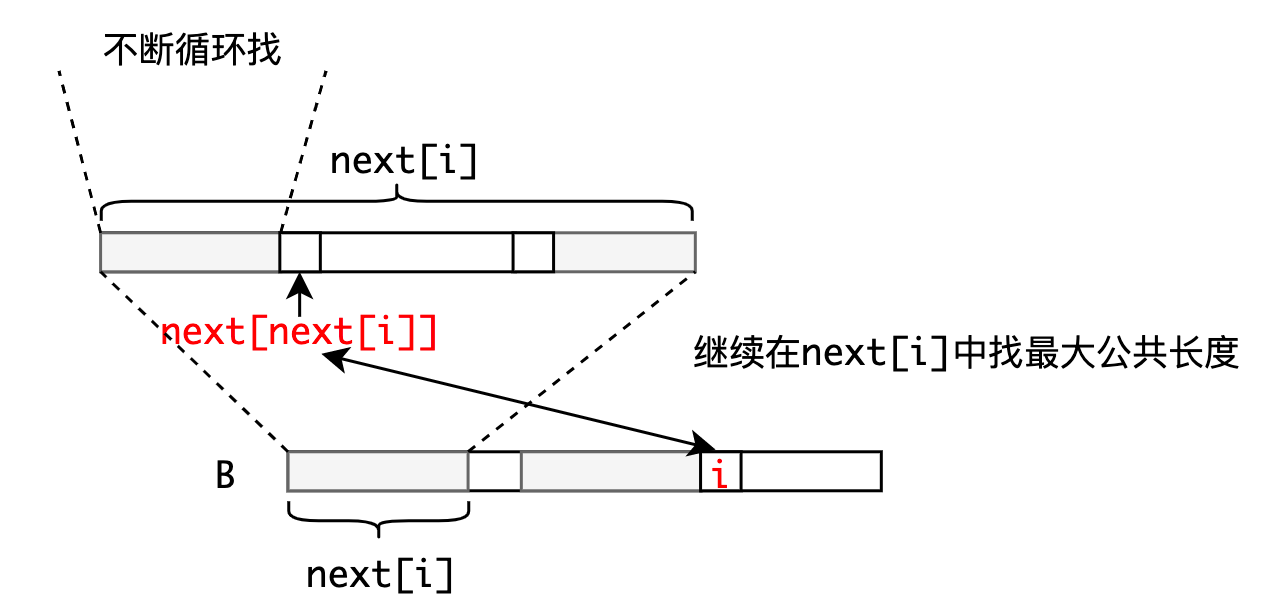
因此，我们得到求$KMP$算法中$next$数组的方法

int n[N];
void getNext(string B) {
    int n = B.size();
    ne[0] = ne[1] = 0;
    for (int i = 1, j = 0; i < n; i++) {
        // j每次循环开始都表示next[i]的值
        while (j && B[i] != B[j])
            j = ne[j];
        if (B[i] == B[j])
            j++;
        ne[i + 1] = j;
    }
}

字符串匹配

在计算完成$next$数组后，我们就可以利用$next$数组在字符串$A$中寻找字符串$B$出现的位置。匹配的代码其实和求$next$数组的代码非常相似，因为匹配过程和求$next$数组的过程其实是一致的

• 设现在字符串$B$的前$i$个位置都和从某个位置开始的字符串$A$匹配，现在比较第$i+1$个位置
• 如果第$i+1$个位置相同，接着比较第$i+2$个位置
• 如果第$i+1$个位置不同，则出现不匹配，我们依旧要将长度为$i$的字符串分割，获得其最大公共长度$next[i]$，然后从$next[i]$继续比较两个字符串

因此，完整的$KMP$算法如下：

/**
 * @file KMP.cpp
 * @author Rick (Kay_Rick@outlook.com)
 * @version 1.0
 * @date 2020-12-15 21:51:49
 * @brief KMP算法
 * 
 * @copyright Copyright (c) 2020 Rick, All Rights Reserved.
 * 
 */
#include <iostream>
#include <string>

using namespace std;

const int N = 100010;
// next数组
int ne[N];
string A, B;

/**
 * @brief Get the Next object
 * @param str 
 */
void getNext(string str) {
    ne[0] = ne[1] = 0;
    for (int i = 1, j = 0; i < str.size(); i++) {
        // j每次循环开始都表示next[i]的值
        while (j > 0 && str[i] != str[j])
            j = ne[j];
        if (str[i] == str[j])
            j++;
        ne[i + 1] = j;
    }
}

int main() {
    cin >> A >> B;
    // 求B的next数组
    getNext(B);
    // KMP匹配过程，j从0开始
    for (int i = 0, j = 0; i < A.size(); i++) {
        // 没有匹配上，j后退到next[j]的位置
        while (j > 0 && A[i] != B[j])
            j = ne[j];
        // 匹配上了
        if (A[i] == B[j])
            j++;
        if (j == B.size()) {
            // 输出匹配起点位置
            cout << i - j + 1 << endl;
            // j往后面走，继续匹配看是否还存在匹配的串
            j = ne[j];
        }
    }
    return 0;
}