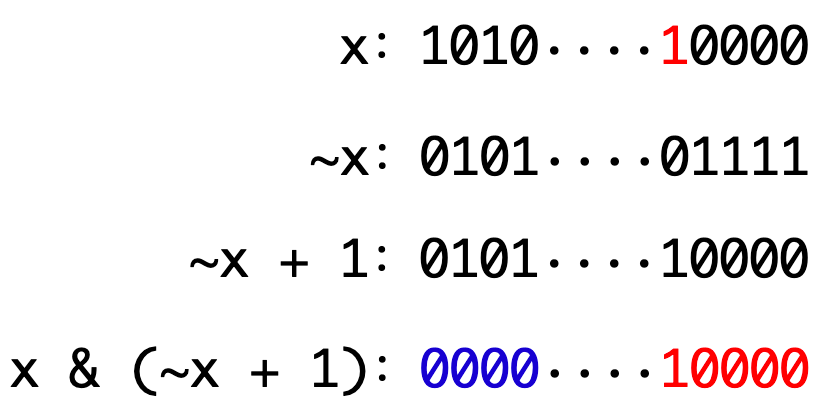在计算机内部都是使用0和1这样二进制来进行存储数据,那么对于很多操作,我们可以通过相关位运算来进行实现,这里就位运算的相关技巧进行一个总结
基本原理
x ∧ 00000000 = x , x & 00000000 = 0 , x ∣ 00000000 = x x \ ^{\land} \ 00000000 = x , x \ \& \ 00000000 = 0 , x\ |\ 00000000 = x x ∧ 0 0 0 0 0 0 0 0 = x , x & 0 0 0 0 0 0 0 0 = 0 , x ∣ 0 0 0 0 0 0 0 0 = x x ∧ 11111111 = ∼ x , x & 11111111 = x , x ∣ 11111111 = 11111111 x \ ^{\land} \ 11111111 = \sim x , x \ \& \ 11111111 = x , x\ |\ 11111111 = 11111111 x ∧ 1 1 1 1 1 1 1 1 = ∼ x , x & 1 1 1 1 1 1 1 1 = x , x ∣ 1 1 1 1 1 1 1 1 = 1 1 1 1 1 1 1 1 x ∧ x = 0 , x & x = x , x ∣ x = x x \ ^{\land} \ x = 0 , x \ \&\ x = x , x\ |\ x = x x ∧ x = 0 , x & x = x , x ∣ x = x > > n >> n > > n 2 n 2n 2 n − 7 > > 2 = − 2 -7 >> 2 = -2 − 7 > > 2 = − 2 > > > n >>>n > > > n 0 0 0 − 7 > > > 2 = 1073741822 -7 >>> 2 = 1073741822 − 7 > > > 2 = 1 0 7 3 7 4 1 8 2 2 < < n << n < < n 2 n 2n 2 n − 7 < < 2 = − 28 -7 << 2 = -28 − 7 < < 2 = − 2 8
运算技巧
根据这些特点,部分操作就显得非常容易
∧ ^{\land} ∧ x ∧ 11111111 = ∼ x x \ ^{\land} \ 11111111 = \sim x x ∧ 1 1 1 1 1 1 1 1 = ∼ x 三个数中重复的两个数去除,只留下另一个数 :利用x ∧ 00000000 = x , x ∧ x = 0 x \ ^{\land} \ 00000000 = x, x \ ^{\land} \ x = 0 x ∧ 0 0 0 0 0 0 0 0 = x , x ∧ x = 0 & \& & n u m num n u m m a s k : 00111100 mask:00111100 m a s k : 0 0 1 1 1 1 0 0 n u m num n u m m a s k mask m a s k 1 1 1 ∣ | ∣ n u m num n u m m a s k : 00111100 mask:00111100 m a s k : 0 0 1 1 1 1 0 0 n u m num n u m m a s k mask m a s k 1 1 1 1 1 1 n & ( n − 1 ) n\ \&\ (n - 1) n & ( n − 1 ) n n n 1 1 1 01011011 01011011 0 1 0 1 1 0 1 1 1 1 1 01011010 01011010 0 1 0 1 1 0 1 0 01011010 01011010 0 1 0 1 1 0 1 0 − n = ∼ n + 1 -n = \sim n + 1 − n = ∼ n + 1 n & ( − n ) n\ \&\ (-n) n & ( − n ) n n n 1 1 1
求第k位数
例如:n = 15 = ( 1111 ) 2 n = 15 = (1111)_{2} n = 1 5 = ( 1 1 1 1 ) 2
先把第k k k x = n > > k x = n >> k x = n > > k
看最后一位是多少:x & 1 x\ \& \ 1 x & 1
因此要取最后一位元素:x = n > > k & 1 x = n >> k\ \& \ 1 x = n > > k & 1
#include <iostream>
using namespace std;
int main() {
int n = 10;
// 从最高位输出:就是输出其二进制表示
for (int k = 3; k >= 0; k--)
cout << (n >> k & 1);
return 0;
}
lowbit(x)
l o w b i t ( x ) lowbit(x) l o w b i t ( x ) x x x 1 1 1 x = 1010 , l o w b i t ( x ) = 10 , x = 101000 , l o w b i t ( x ) = 1000 x = 1010, lowbit(x) = 10, x = 101000, lowbit(x) = 1000 x = 1 0 1 0 , l o w b i t ( x ) = 1 0 , x = 1 0 1 0 0 0 , l o w b i t ( x ) = 1 0 0 0
− x = ∼ x + 1 -x = \sim x + 1 − x = ∼ x + 1
有了l o w b i t ( x ) lowbit(x) l o w b i t ( x ) x x x 1 1 1
#include <iostream>
using namespace std;
int lowbit(int x) {
return x & (-x);
}
int main() {
int x, ans = 0;
scanf("%d", &x);
while (x) {
x -= lowbit(x);
ans++;
}
printf("%d ", ans);
return 0;
}