高精度算法分析

高精度运算：是指参与运算的数(加数，减数，因子……）范围大大超出了标准数据类型（整型，实型）能表示的范围的运算。例如，求两个20000位的数的和。这时，就要用到高精度算法了

高精度加法

• 若t1表示第一个数当前位数的大小，t2表示第二个数当前位数的大小，t表示进位数

• 从个位数开始进行相加，使用t记录(t1 + t2 + next)得出的结果，t % 10为该位数确定好的元素，进行下一个位数操作时，需要t /= 10

#include <iostream>
#include <vector>
#include <string>

using namespace std;

const int N = 1e6 + 10;

vector<int> add(vector<int>& A, vector<int>& B){
    vector<int> C;
    int t = 0;
    for (int i = 0; i < A.size() || i < B.size(); i++) {
        if (i < A.size())
            t += A[i];
        if (i < B.size())
            t += B[i];
        C.push_back(t % 10);
        t /= 10;
    }
    if (t > 0)
        C.push_back(1);
    return C;
}

int main() {
    string a, b;
    cin >> a >> b;
    // 高精度数据反向存储在数组中
    vector<int> A, B;
    for (int i = a.size() - 1; i >= 0; i--)
        A.push_back(a[i] - '0');
    for (int i = b.size() - 1; i >= 0; i--) 
        B.push_back(b[i] - '0');
    vector<int> result = add(A, B);
    
    for (int i = result.size() - 1; i >= 0; i--)
        cout << result[i];
    cout << endl;
    return 0;
}

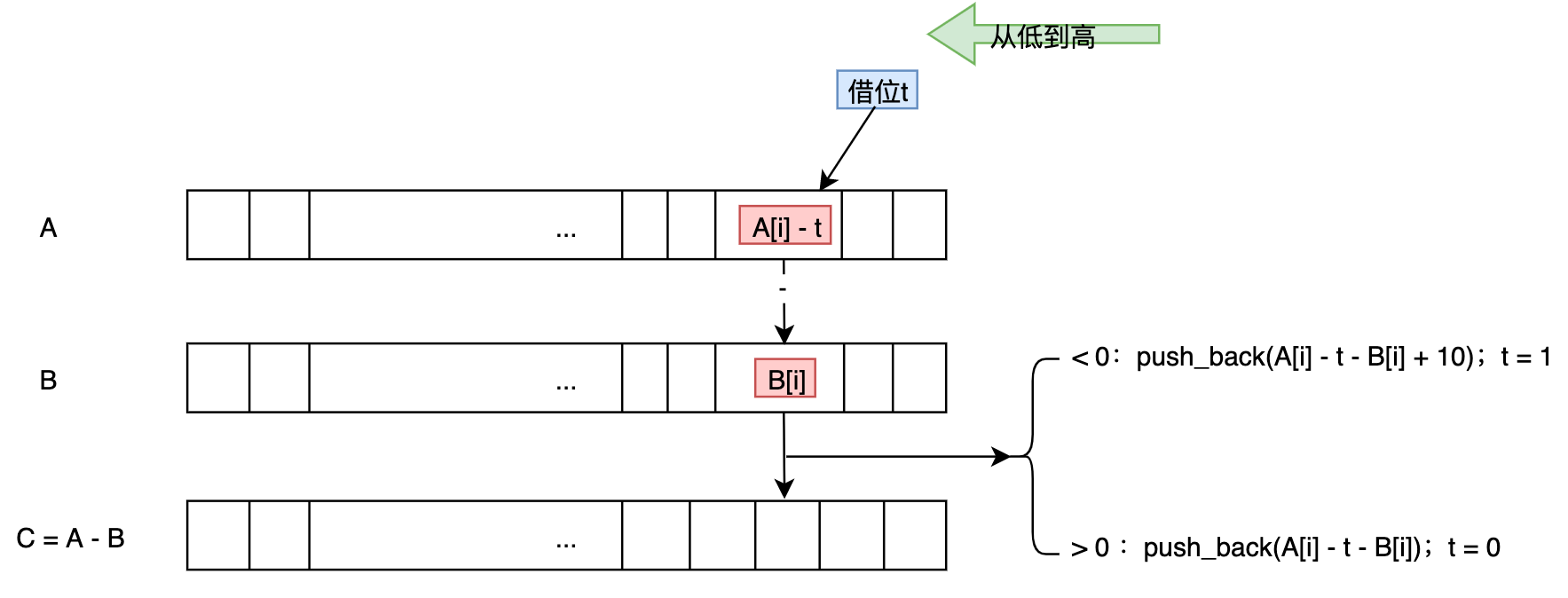
高精度减法

• 我们先比较A和B的大小，我们始终用大的数减去小的数

• 对于 t = A[i] - B[i] - t； 可以拆为 t = A[i] - t如果B[i]合法，再t -= B[i] 这么两步来做

• 去掉高位中的0

#include <iostream>
#include <vector>
#include <string>

using namespace std;

// 判断A >= B是否满足
bool cmp(vector<int>& A, vector<int>& B) {
    if (A.size() != B.size())
        return A.size() > B.size();
    else {
        for (int i = A.size() - 1; i >= 0; i--) 
            if (A[i] != B[i])
                return A[i] > B[i];
    }
    return true;
}

vector<int> sub(vector<int>& A, vector<int>& B) {
    vector<int> C;
    // 借位
    int t = 0;
    for (int i = 0; i < A.size(); i++) {
        t = A[i] - t;
        // 如果合法
        if (i < B.size())
            t -= B[i];
        // A[i] 这一位够减，没有产生借位
        if (t >= 0) {
            C.push_back(t);
            t = 0;
        }
        else {
            C.push_back(t + 10);
            t = 1;
        }
    }
    // 去掉高位中的0
    while (C.size() > 1 && C.back() == 0)
        C.pop_back();
    return C;
}

int main() {
    string a, b;
    cin >> a >> b;
    vector<int> A, B;
    for (int i = a.size() - 1; i >= 0; i--)
        A.push_back(a[i] - '0');
    for (int i = b.size() - 1; i >= 0; i--)
        B.push_back(b[i] - '0');
    
    // A >= B的情况
    if (cmp(A, B)) {
        vector<int> C = sub(A, B);
        for (int i = C.size() - 1; i >= 0; i--)
            cout << C[i];
    }
    else {
        vector<int> C = sub(B, A);
        cout << '-';
        for (int i = C.size() - 1; i >= 0; i--)
            cout << C[i];
    }
    cout << endl;
    return 0;
}

高精度乘法

• 模拟乘法规则，从A的个位到高位与B相乘，乘得的结果放入t中，则此位的数为t % 10。把t / 10剩余给下一个高位

• 若遍历完整个A，t > 0，则表示还有剩余的数，则需要将剩余的数继续补到下一个高位

• 删除高位出现的0

#include <iostream>
#include <vector>
#include <string>

using namespace std;

vector<int> mul(vector<int>& A, int b) {
    vector<int> C;
    int t = 0;
    for (int i = 0; i < A.size() || t; i++) {
        // 有可能在乘b之后出现进位要多加一位，因此需要判断
        if (i < A.size())
            t += A[i] * b;
        C.push_back(t % 10);
        t /= 10;
    }
    // 删除高位0
    while (C.size() > 1 && C.back() == 0)
        C.pop_back();
    return C;
}

int main() {
    string a;
    int b;
    cin >> a >> b;
    vector<int> A, result;
    
    for (int i = a.size() - 1; i >= 0; i--)
        A.push_back(a[i] - '0');
    result = mul(A, b);
    
    for (int i = result.size() - 1; i >= 0; i--)
        cout << result[i];
    cout << endl;
    return 0;
}

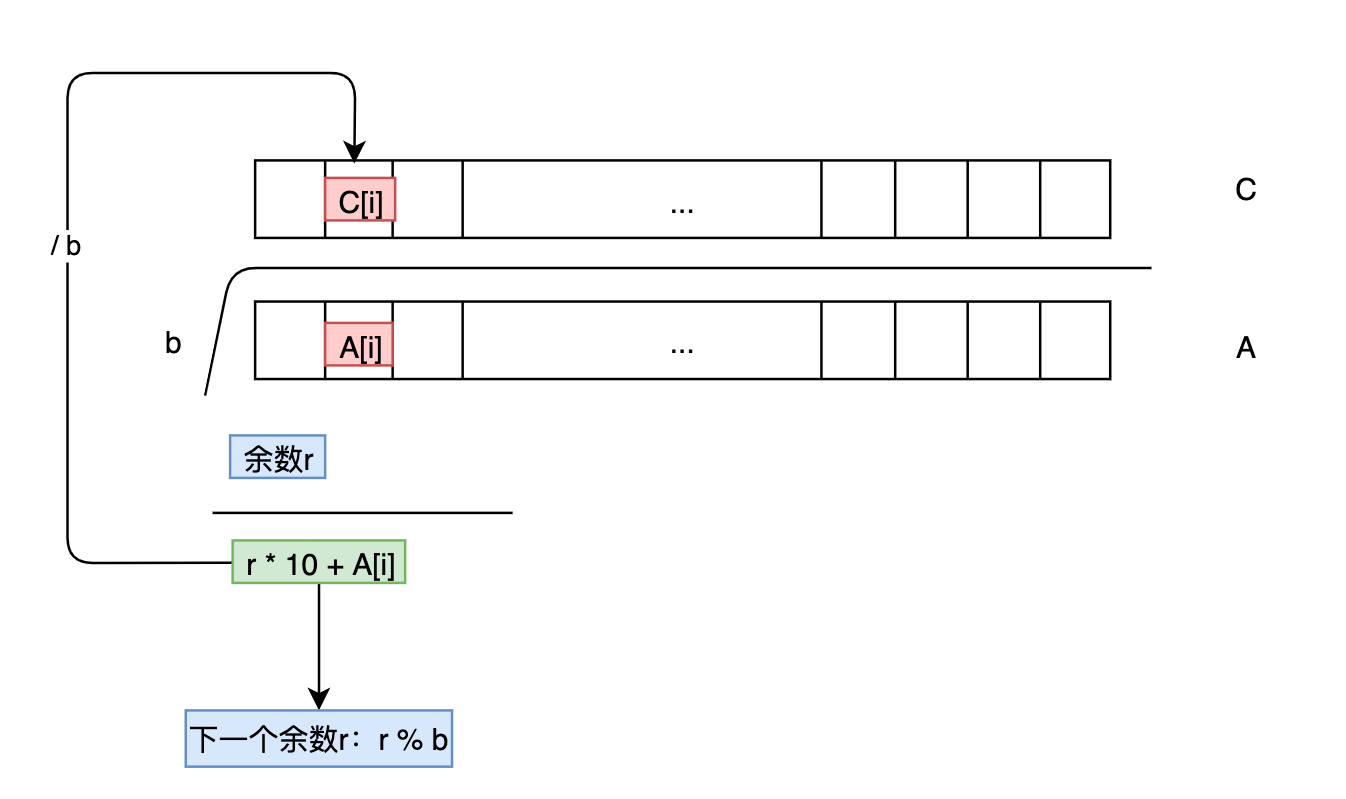
高精度除法

• 模拟除法规则，从高位到底位与除数进行相除，除得的余数放入t中，则此位的数为t / 10，把剩余的t % 10给下一个底位
• 若遍历完整个A，需要将最靠左的且为0的高位全部去除掉

#include <iostream>
#include <vector>
#include <string>
#include <algorithm>

using namespace std;

vector<int> div(vector<int>& A, int b, int& r) {
    vector<int> C;
    // 除法是从最高位开始除
    for (int i = A.size() - 1; i >= 0; i--) {
        r = r * 10 + A[i];
        C.push_back(r / b);
        r %= b; 
    }
    // 与我们逆向存储数据相反，为了统一，reverse
    reverse(C.begin(), C.end());
    // 去除高位的0
    while (C.size() > 1 && C.back() == 0)
        C.pop_back();
    return C;
}


int main() {
    string a;
    int b;
    cin >> a >> b;
    vector<int> A;
    for (int i = a.size() - 1; i >= 0; i--) 
        A.push_back(a[i] - '0');
    int r = 0;
    vector<int> result = div(A, b, r);
    for (int i = result.size() - 1; i >= 0; i--)
        cout << result[i];
    cout << endl << r << endl;
    return 0;
}