从微分积分看前缀和差分

前缀和差分互为逆运算，他们关系很像数学中的微分和积分。这两种算法能有效解决数组某段区间的和以及对某段区间加上一个同一个数的问题，下面介绍其应用场景及模板方法。

前缀和

原数组A： $a[1], a[2], a[3], ... a[n]$，前缀和$s[i]$ 为数组的前i项和（前缀和的下标一定要从1开始，避免进行下表的转换）

作用：快速求出元素组中某段区间的和

一维数组前缀和

• 构造前缀和$s[i] = s[i - 1] + a[i]$
• 求数组A区间$[l, r]$之间的和 $s[r] - s[l - 1]$

输入一个长度为n的整数序列。接下来再输入m个询问，每个询问输入一对l, r。对于每个询问，输出原序列中从第l个数到第r个数的和。

输入格式

第一行包含两个整数n和m。第二行包含n个整数，表示整数数列。接下来m行，每行包含两个整数l和r，表示一个询问的区间范围。

输出格式

共m行，每行输出一个询问的结果。

数据范围

$1≤l≤r≤n, 1≤n,m≤100000, −1000≤ 数列中元素的值 ≤1000$

输入样例：

5 3
2 1 3 6 4
1 2
1 3
2 4

输出样例：

3
6
10

#include <iostream>

using namespace std;
const int N = 100010;
int a[N], S[N];
int n, m;

int main() {
    cin >> n >> m;
    S[0] = 0;
    for (int i = 1; i <= n; i++) {
        cin >> a[i];
        S[i] = S[i - 1] + a[i];
    }
    while (m--) {
        int l, r;
        cin >> l >> r;
        cout << S[r] - S[l - 1] << endl;
    }
    return 0;
}

二维数组前缀和

• 求前缀和$S[i] [j] = s[i - 1][j] + s[i] [j - 1] - s[i - 1] [j - 1] + a[i] [j]$

• 求解子矩阵$(x1, y1), (x2, y2)$的和子矩阵中的和$s[x2] [y2] - s[x2] [y1 - 1] - s[x1 - 1] [y2] + s[x1 - 1] [y1 - 1]$

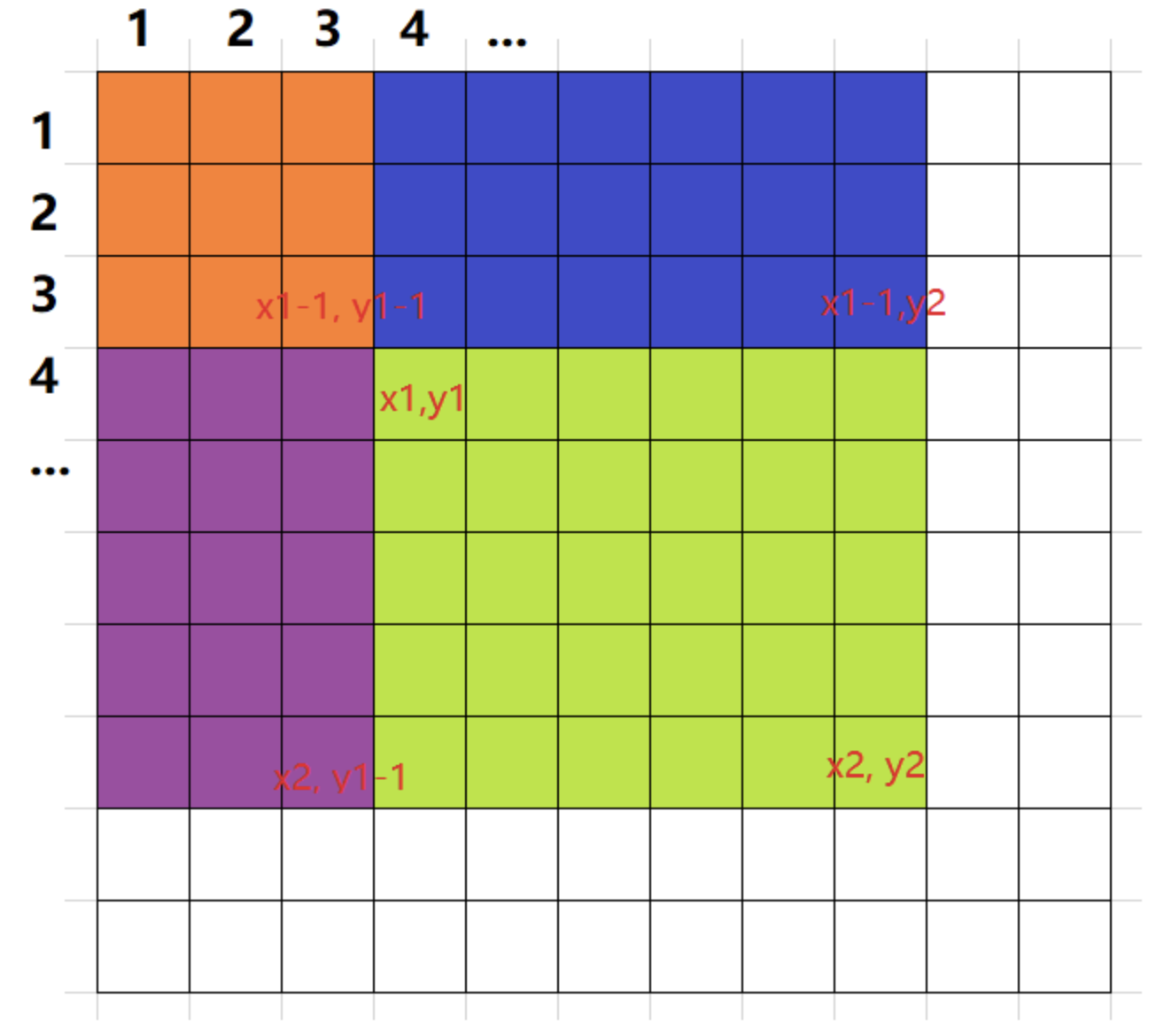
输入一个n行m列的整数矩阵，再输入q个询问，每个询问包含四个整数x1, y1, x2, y2，表示一个子矩阵的左上角坐标和右下角坐标。对于每个询问输出子矩阵中所有数的和。

输入格式

第一行包含三个整数n，m，q。接下来n行，每行包含m个整数，表示整数矩阵。接下来q行，每行包含四个整数x1, y1, x2, y2，表示一组询问。

输出格式

共q行，每行输出一个询问的结果。

数据范围

$1≤n,m≤1000, 1≤q≤200000, 1≤x1≤x2≤n, 1≤y1≤y2≤m, −1000≤矩阵内元素的值≤1000$

输入样例：

3 4 3
1 7 2 4
3 6 2 8
2 1 2 3
1 1 2 2
2 1 3 4
1 3 3 4

输出样例：

17
27
21

#include <iostream>

using namespace std;
const int N = 1010;
int a[N][N], s[N][N];
int n, m, q;

int main() {
    cin >> n >> m >> q;
    s[0][0] = 0;
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= m; j++) {
            cin >> a[i][j];
            s[i][j] = s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1] + a[i][j];
        }
    }
    
    while (q--) {
        int x1, y1, x2, y2;
        cin >> x1 >> y1 >> x2 >> y2;
        cout << s[x2][y2] - s[x2][y1 - 1] - s[x1 - 1][y2] + s[x1 - 1][y1 - 1] << endl;
    }
    return 0;
}

差分

原数组A： $a[1], a[2], a[3], ... a[n]$ ，构造数组B： $b[1], b[2], b[3], ... b[n]$ 使得$a[i] = b[1] + b[2] + b[3] + ... + b[i]$

应用：使数组A的$[l ,r]$区间都加上c，我们只需要使$b[l] += c, b[r + 1] -= c$，然后通过前缀和再求原数组就完成运算，时间复杂度从$O(n)$ 优化至$O(1)$

一维差分

输入一个长度为n的整数序列。接下来输入m个操作，每个操作包含三个整数l, r, c，表示将序列中[l, r]之间的每个数加上c。请你输出进行完所有操作后的序列。

输入格式

第一行包含两个整数n和m。第二行包含n个整数，表示整数序列。接下来m行，每行包含三个整数l，r，c，表示一个操作。

输出格式

共一行，包含n个整数，表示最终序列。

数据范围

$1≤n,m≤100000, 1≤l≤r≤n, −1000≤c≤1000, −1000≤整数序列中元素的值≤1000$

输入样例：

6 3
1 2 2 1 2 1
1 3 1
3 5 1
1 6 1

输出样例：

3 4 5 3 4 2

#include<iostream>

using namespace std;

const int N = 100010;
int s[N], b[N];
int n, m;

int main(){
    cin >> n >> m;
    for(int i = 1;i <= n;i++) 
        cin >> s[i];

    //构造差分数组
    for(int i = 1;i <= n;i++) 
        b[i] = s[i] - s[i - 1];

    while(m--){
        int l, r, c;
        cin >> l >> r >> c;
        b[l] += c;//将l和以后加c
        b[r + 1] -= c;//将r之后-c
    }

    for(int i = 1;i <= n; i++){
        b[i] = b[i - 1] + b[i];//将差分改为原数组
        cout << b[i] << ' ';
    }
    return 0;
}

二维差分

• $b[x1] [y1] += c$
• $b[x2 + 1] [y1] -= c$
• $b[x1] [y2 + 1] -= c$
• $b[x2 + 1] [y2 + 1] += c$

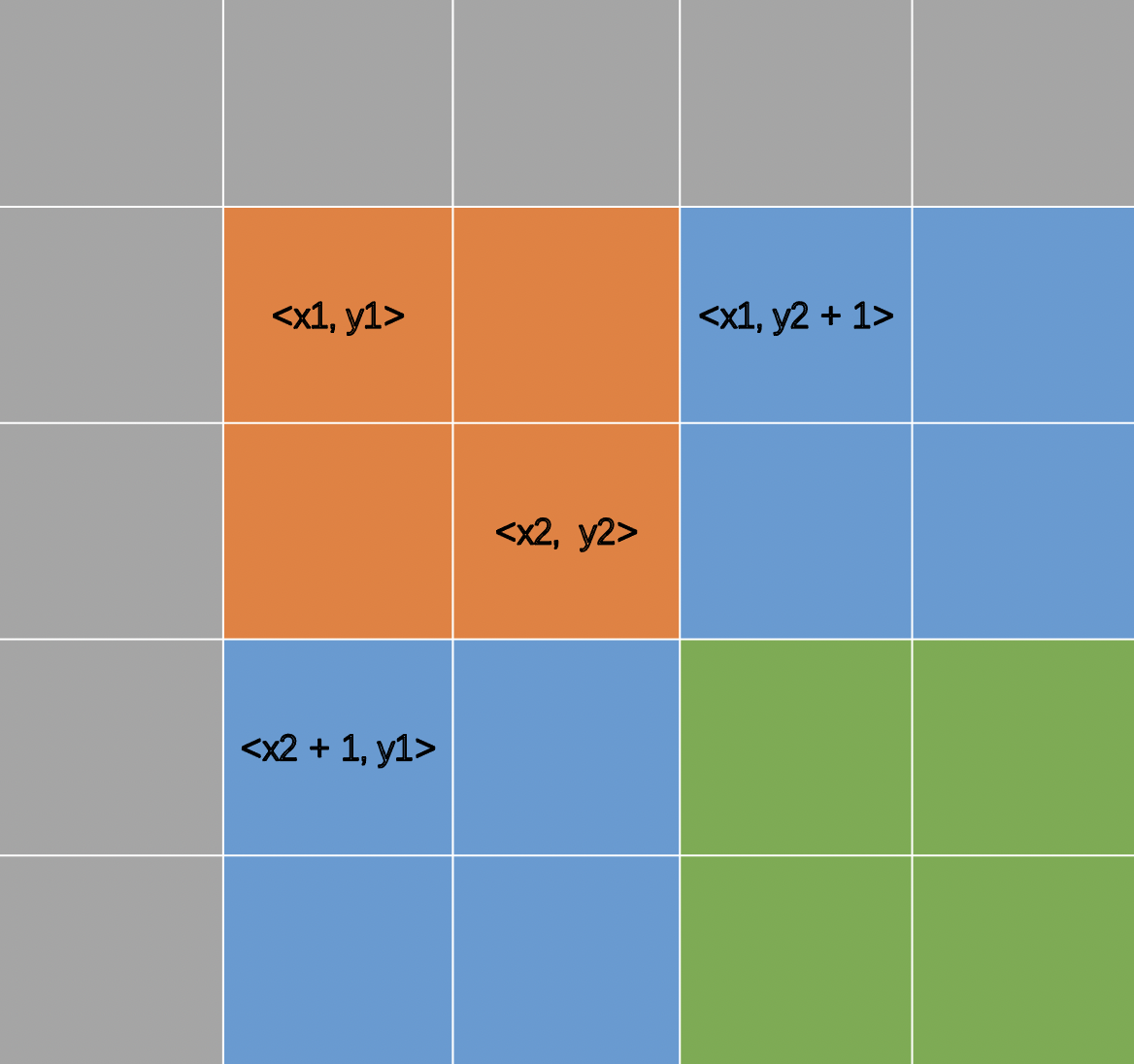
输入一个n行m列的整数矩阵，再输入q个操作，每个操作包含五个整数x1, y1, x2, y2, c，其中(x1, y1)和(x2, y2)表示一个子矩阵的左上角坐标和右下角坐标。每个操作都要将选中的子矩阵中的每个元素的值加上c。请你将进行完所有操作后的矩阵输出。

输入格式

第一行包含整数n,m,q。接下来n行，每行包含m个整数，表示整数矩阵。接下来q行，每行包含5个整数x1, y1, x2, y2, c，表示一个操作。

输出格式

共 n 行，每行 m 个整数，表示所有操作进行完毕后的最终矩阵。

数据范围

$1≤n,m≤1000, 1≤q≤100000, 1≤x1≤x2≤n, 1≤y1≤y2≤m, −1000≤c≤1000, −1000≤矩阵内元素的值≤1000$

输入样例：

3 4 3
1 2 2 1
3 2 2 1
1 1 1 1
1 1 2 2 1
1 3 2 3 2
3 1 3 4 1

输出样例：

2 3 4 1
4 3 4 1
2 2 2 2

#include<iostream>
using namespace std;

const int N = 1010;
int a[N][N], b[N][N];
int n, m, q;

int main() {
    cin >> n >> m >> q;
    for(int i = 1; i <= n; i++)
        for(int j = 1; j <= m; j++)
            cin >> a[i][j];
    // 计算差分数组
    for(int i = 1; i <= n; i++)
        for(int j = 1; j <= m; j++) {
            b[i][j] += a[i][j];
            b[i + 1][j] -= a[i][j];
            b[i][j + 1] -= a[i][j];
            b[i + 1][j + 1] += a[i][j];
        }

    while(q--) {
        int x1, y1, x2, y2, c;
        cin >> x1 >> y1 >> x2 >> y2 >> c;
        b[x1][y1] += c;
        b[x2 + 1][y1] -= c;
        b[x1][y2 + 1] -= c;
        b[x2 + 1][y2 + 1] += c;
    }
    //对差分求前缀和
     for(int i = 1; i <= n; i++) {
        for(int j = 1; j <= m; j++) {
            b[i][j] += b[i][j - 1] + b[i - 1][j] - b[i - 1][j - 1];
            cout << b[i][j] << " ";
        }
        cout << endl;
     }
    return 0;
}