从暴力枚举到双指针算法

双指针算法：双指针是算法编程中一种非常重要的算法思想。所谓双指针算法，就是指的是在遍历的过程中，不是普通的使用单个指针进行循环访问，而是使用两个相同方向或者相反方向的指针进行扫描，从而达到相应的目的。通常使用双指针算法解决的第一大类问题是：对$O(n^2)$的枚举进行优化到$O(n)$

模板

暴力枚举模板

for (int i = 0; i < n; i++) 
    for (int j = 0; j < n; j++)
        ...

双指针模板

• 双指针的核心在于找题目中找另一个指针的单调性来降低题目的复杂度

for (int i = 0, j = 0; i < n; i++) {
    while (j < i && check(i, j))
        j++;
    // 每道题具体逻辑
}

数组元素目标和

给定两个升序排序的有序数组$A$和$B$，以及一个目标值$x$。数组下标从$0$开始。请你求出满足$A[i] + B[j] = x$的数对$(i, j)$。数据保证有唯一解。

输入格式

第一行包含三个整数$n，m，x$分别表示$A$的长度，$B$的长度以及目标值$x$。第二行包含$n$个整数，表示数组$A$。第三行包含$m$个整数，表示数组$B$。

输出格式

共一行，包含两个整数 $i$ 和 $j$。

数据范围

数组长度不超过$100000$。同一数组内元素各不相同。$1≤ 数组元素 ≤10^9$

输入样例：

4 5 6
1 2 4 7
3 4 6 8 9

输出样例：

1 1

暴力枚举

for (int i = 0; i < n; i++)
    for (int j = 0; j < m; j++)
        if (a[i] + b[j] == x) 
            cout << i << ' ' << j << endl;

双指针

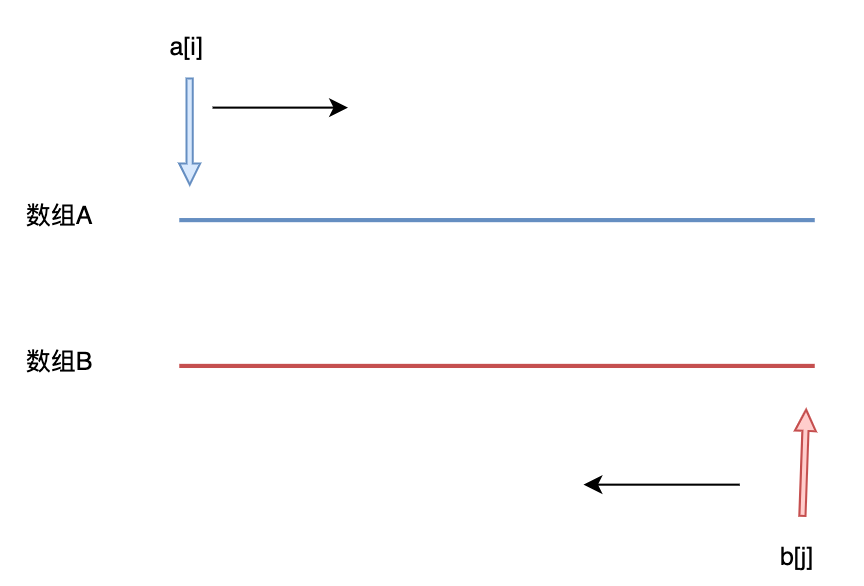
• 找到单调性：$A$和$B$数组都是单调上升，因此我们发现针对每一个$A[i]$都去找一个$B[j]$，使得$A[i]+ B[j] >= x$并且$j$是最靠左的那一个下标。那么我们的$j$就从$B$的尾部往前走

#include <iostream>

using namespace std;

const int N = 100010;
int n, m, x;
int a[N], b[N];

int main() {
    cin >> n >> m >> x;
    for (int i = 0; i < n; i++)
        cin >> a[i];
    for (int i = 0; i < m; i++)
        cin >> b[i];
    for (int i = 0, j = m - 1; i < n; i++) {
        while (j >= 0 && a[i] + b[j] > x)
            j--;
        if (j >= 0 && a[i] + b[j] == x) {
            cout << i << ' ' << j << endl;
            break;
        }
    }
    return 0;
}

最长连续不重复子序列

给定一个长度为n的整数序列，请找出最长的不包含重复的数的连续区间，输出它的长度。

输入格式

第一行包含整数n。第二行包含n个整数（均在0~100000范围内），表示整数序列。

输出格式

共一行，包含一个整数，表示最长的不包含重复的数的连续区间的长度。

数据范围

$1≤n≤100000$

输入样例：

5
1 2 2 3 5

输出样例：

3

暴力枚举

for (int i = 0; i < n; i++)
    for (int j = 0; j <= i; j++)
        if (check(j, i))	// 检查[j, i]这一段是否满足
            res = max(res, i - j + 1);

双指针算法

• 遍历数组a中的每一个元素$a[i]$，对于每一个$i$，找到j使得双指针$[j,\ i]$维护的是以$a[i]$结尾的最长连续不重复子序列，长度为$i - j + 1$, 将这一长度与$res$的较大者更新给$res$
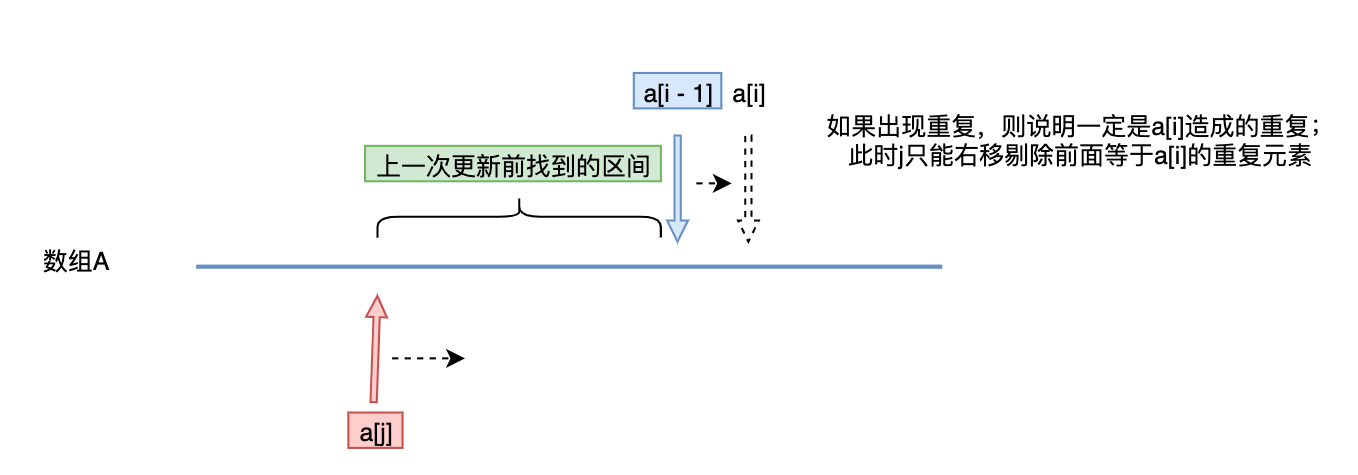
• 单调性：对于每一个$i$，如何确定$j$的位置：由于$[j,\ i - 1]$是前一步得到的最长连续不重复子序列，所以如果$[j,\ i]$中有重复元素，一定是$a[i]$，因此右移$j$直到$a[i]$不重复为止（由于$[j,\ i - 1]$已经是前一步的最优解，此时$j$只可能右移以剔除重复元素$a[i]$，不可能左移增加元素，因此，$j$具有单调性）
• 用数组$s$记录子序列$a[j,\ i]$中各元素出现次数，遍历过程中对于每一个$i$有$3$步操作：
  • 将$a[i]$出现次数$cnt[a[i]]$加$1$
  • 若$a[i]$重复则右移$j$直到不出现重复（$cnt[a[j]]$要减$1$）
  • 确定$j$及更新当前长度$i - j + 1$给$res$

#include <iostream>

using namespace std;

const int N = 100010;
int a[N], cnt[N];
int n;

int main() {
    cin >> n;
    for (int i = 0; i < n; i++) 
        cin >> a[i];
    
    int res = 0;
    for (int i = 0, j = 0; i < n; i++) {
        cnt[a[i]]++;
        while (s[a[i]] > 1) {
            cnt[a[j]]--;
            j++;
        }
        res = max(res, i - j + 1);
    }
    cout << res << endl;
    return 0;
}